Дискриминант квадратного уравнения позволяет различать не только отличников и троечников, но и квадратные уравнения с двумя корнями и квадратные уравнения без действительных корней. В сюжете Дискриминант, который следует понять перед изучением предлагаемого фильма, рассказывается и о связанной с этим геометрии.
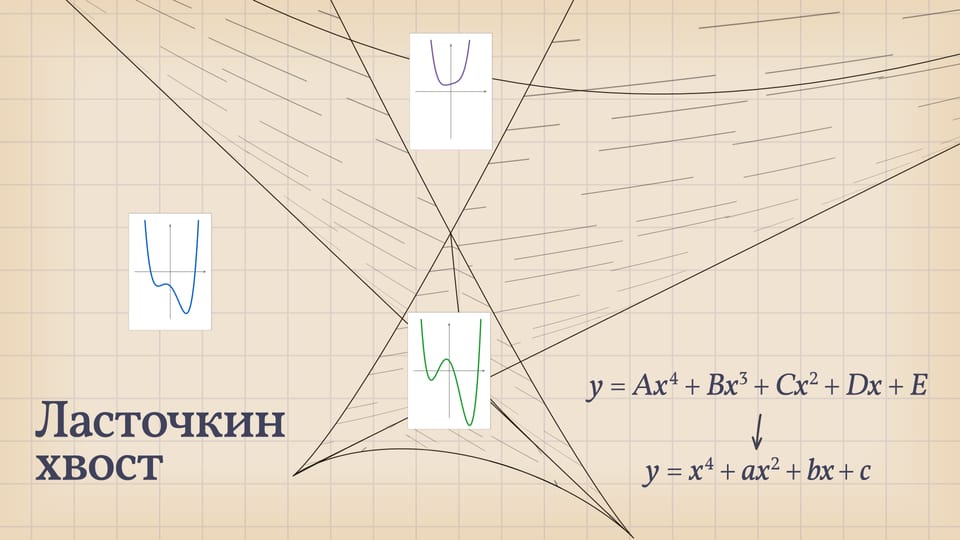
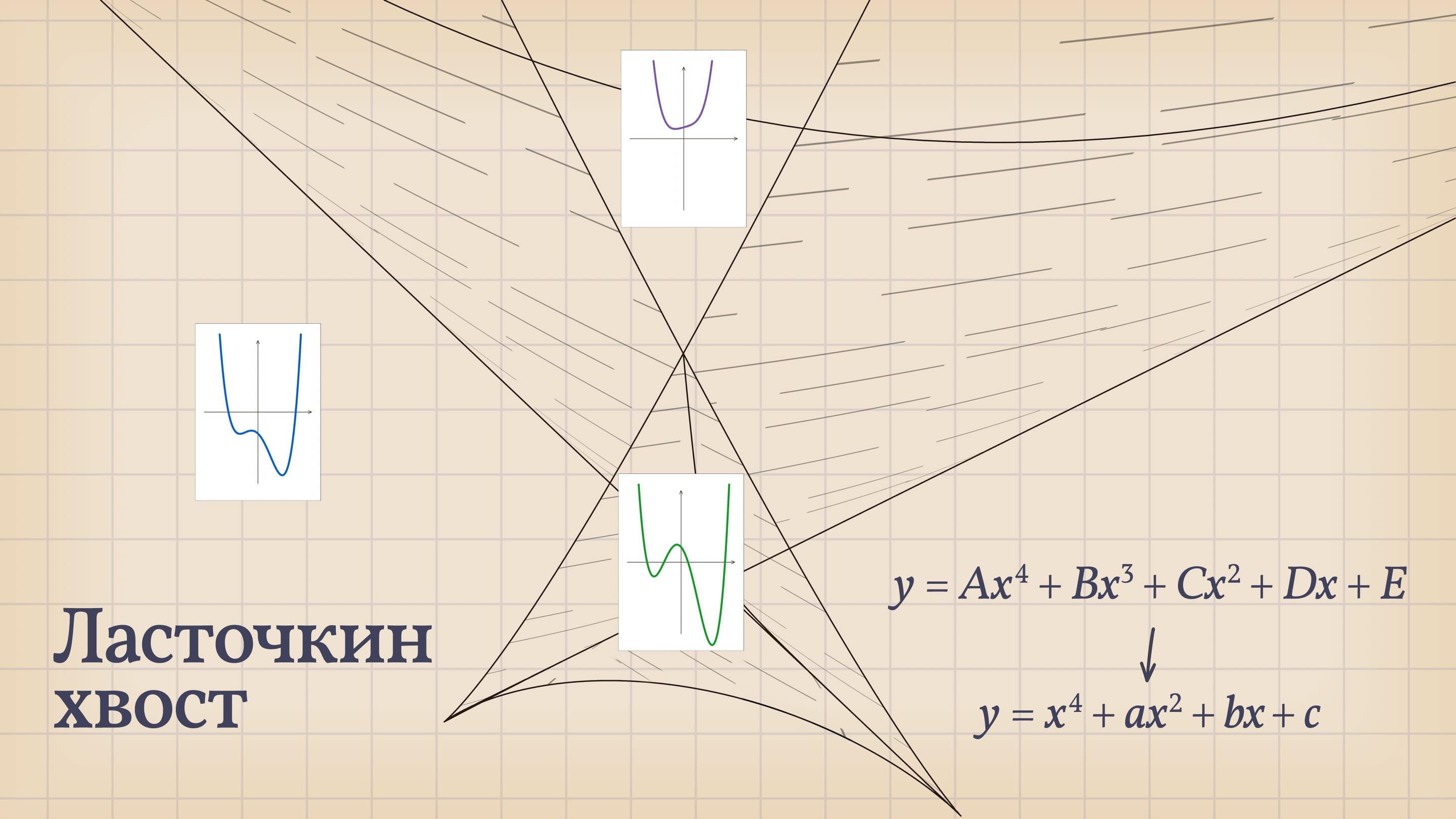
В мире уравнений четвёртой степени уравнения с разным количеством корней разделяет «ласточкин хвост» — дискриминантная поверхность, «живущая» в трёхмерном пространстве.
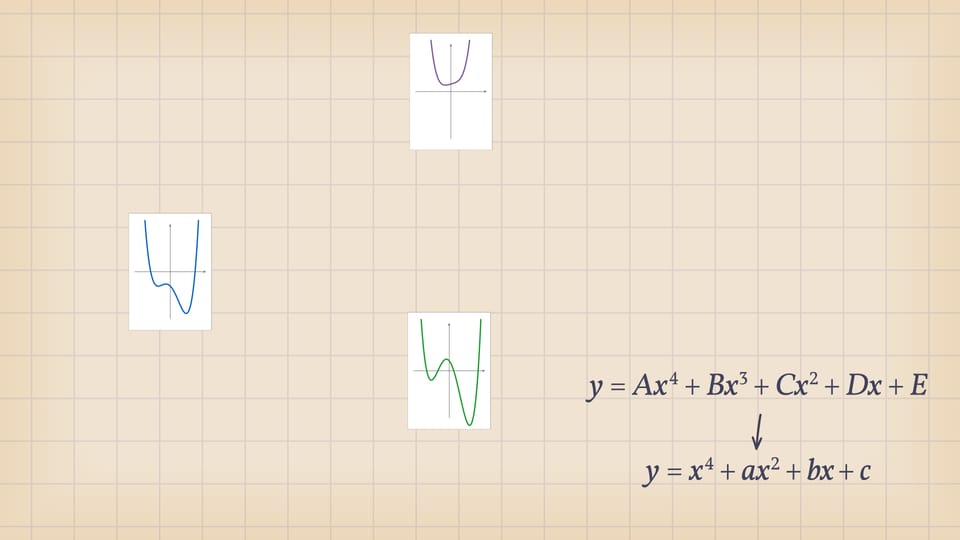
Уравнение четвёртой степени $Ax^4+Bx^3+Cx^2+Dx+E=0$ имеет геометрического двойника: на плоскости $Oxy$ уравнению соответствует график функции $y=Ax^4+Bx^3+Cx^2+Dx+E$, нули которой — пересечения графика с осью $Ox$ — решения соответствующего уравнения. Делением на коэффициент при старшей степени (растяжением по оси $Oy$) и сдвигом по $x$ любое уравнение четвёртой степени можно привести к виду $x^4+ax^2+bx+c=0$: количество корней не поменяется, график качественно будет выглядеть так же, а коэффициентов-параметров меньше.
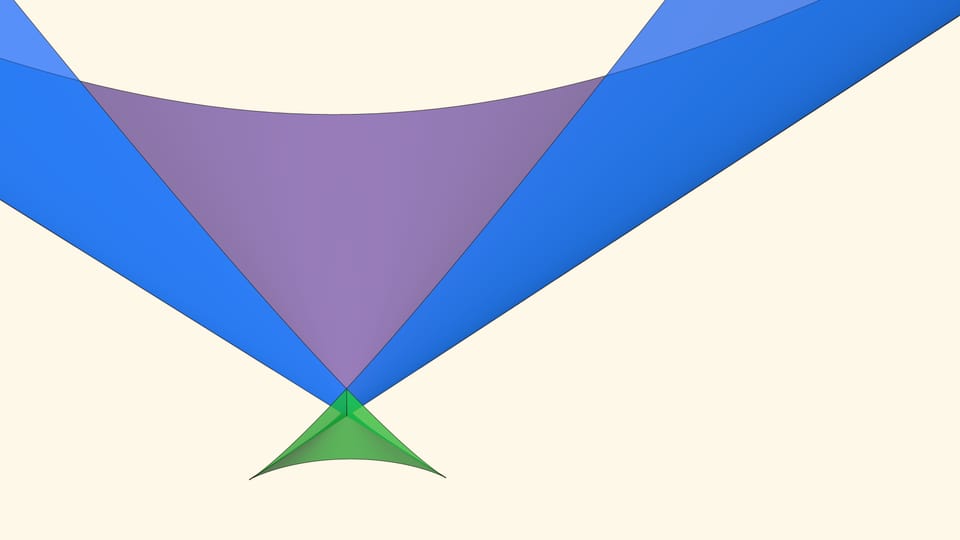
Значит, мир уравнений четвёртой степени имеет «трёхмерное» описание: каждое уравнение $x^4+ax^2+bx+c=0$ кодируется точкой $(a,b,c)$ в трёхмерном пространстве параметров. И в зависимости от положения этой точки количество действительных корней «типичного» уравнения четвёртой степени — точек пересечений графика с осью $Ox$ — может быть 4 или 2, или вообще 0. Разделяет эти случаи «ласточкин хвост» — дискриминантная поверхность, образованная точками, отвечающими уравнениям с кратными действительными корнями. При переходе из одной из областей, на которые делит пространство параметров дискриминантная поверхность, в другую точка параметров оказывается на самой поверхности. В этот момент некоторые корни сливаются, график касается оси $Ox$ и реализуются ещё случаи, когда корней у уравнения 3 или 1.
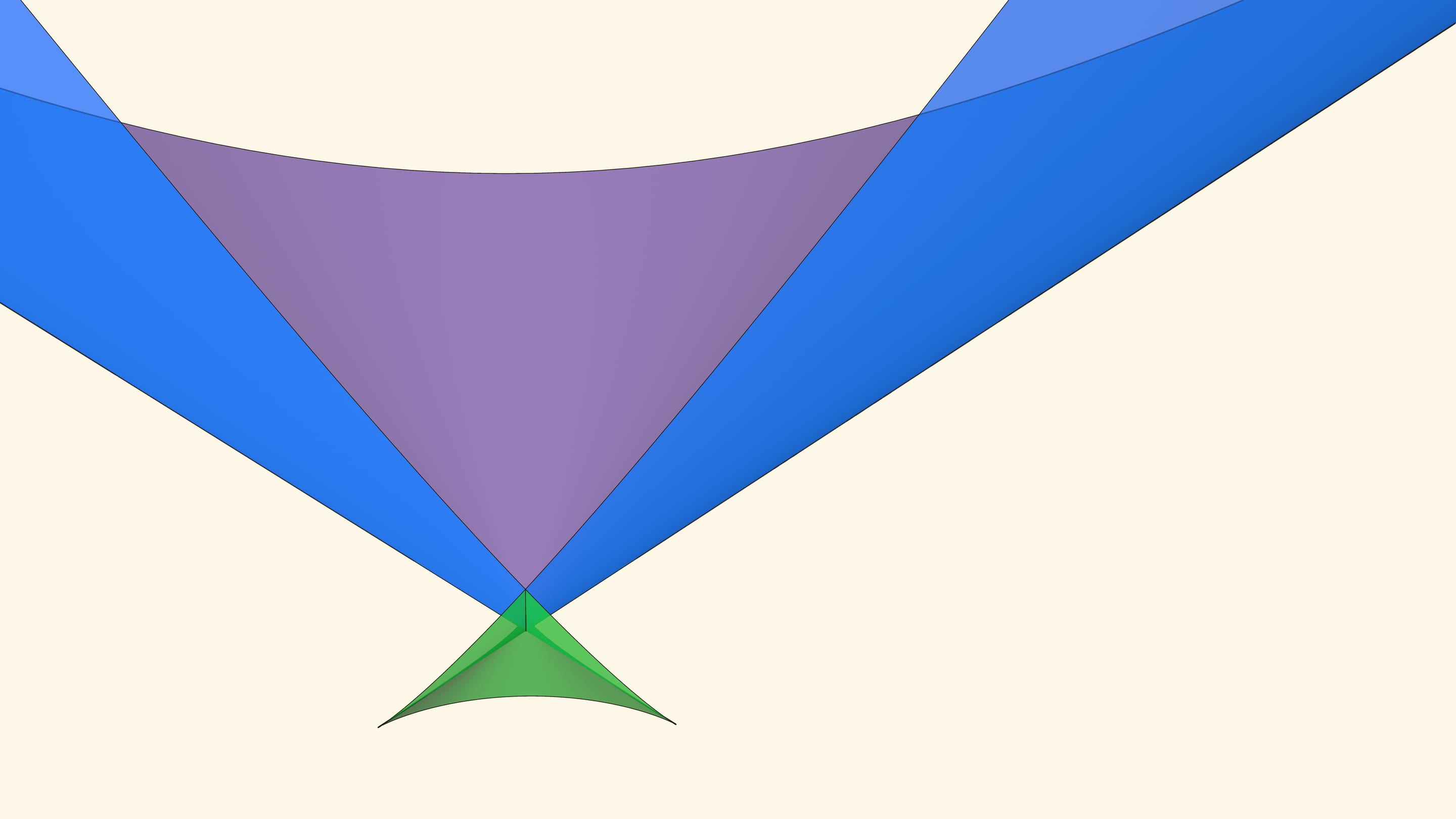
В большинстве своих точек ласточкин хвост — это гладкая поверхность, но есть идущая вверх линия самопересечения, а также две половинки полукубического ребра возврата. Расходясь от «вершины» поверхности, эти три линии образуют криволинейный трёхгранный угол.
Сечения вертикальной плоскостью ласточкиного хвоста в зелёной части снова похожи на хвост ласточки, когда её рисуют на плоском листе бумаги. Когда плоскость проходит через вершину поверхности, кривая пересечения перестаёт быть самопересекающейся, но у неё есть точка излома, негладкости. Дальше от вершины это уже гладкая линия. (Для знатоков: если смотреть «в обратном времени», то кривые похожи на плоский волновой фронт, например, от параболы — эквидистанты внутрь параболы.)
Ребро возврата имеет вид полукубической кривой. Ласточкин хвост — линейчатая поверхность: заметается прямыми линиями. При этом прямолинейные образующие являются касательными к ребру возврата. И это ещё один способ построения ласточкиного хвоста: стартовать с полукубической кривой в пространстве и рассмотреть все её касательные.
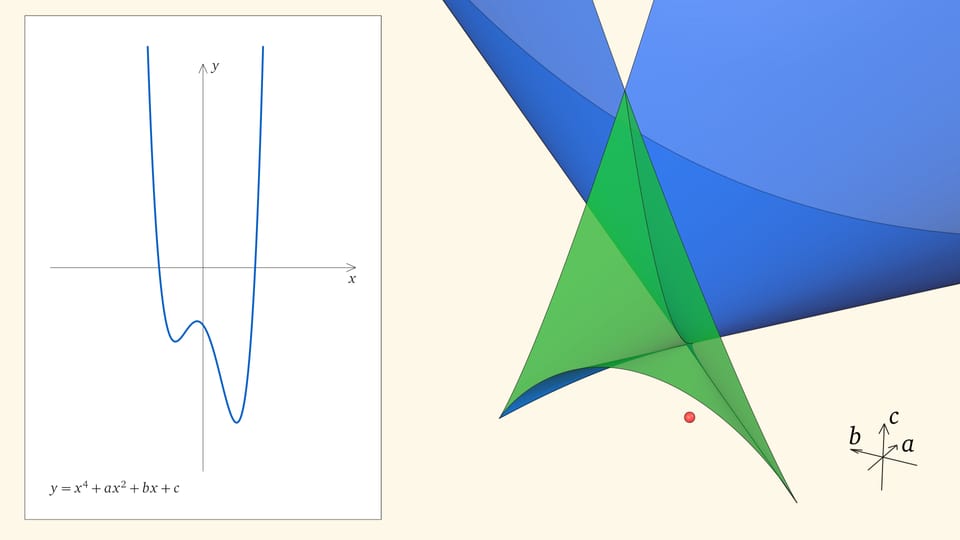
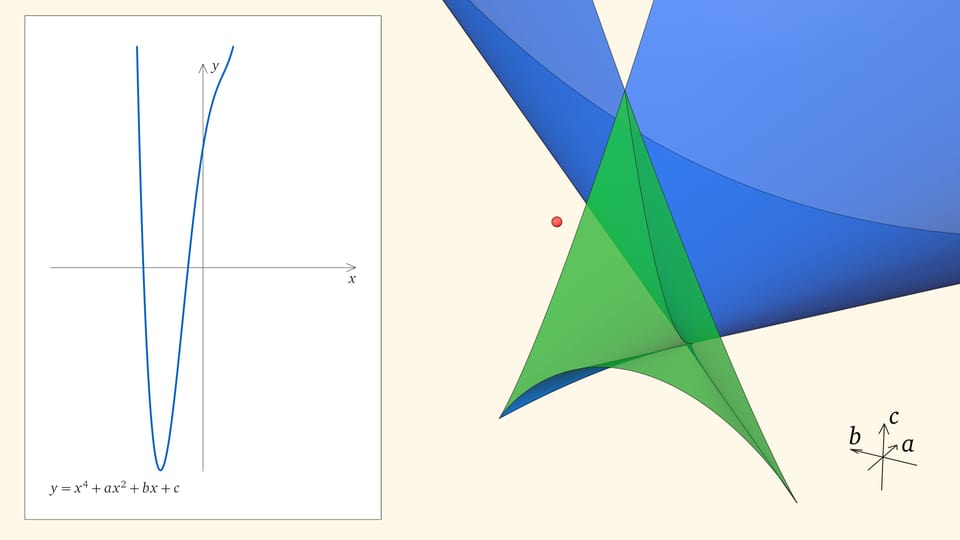
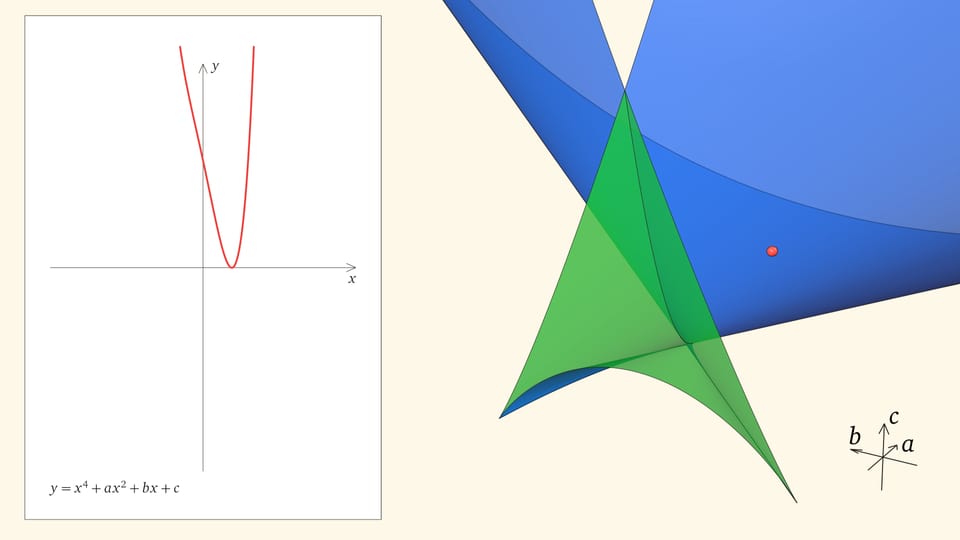
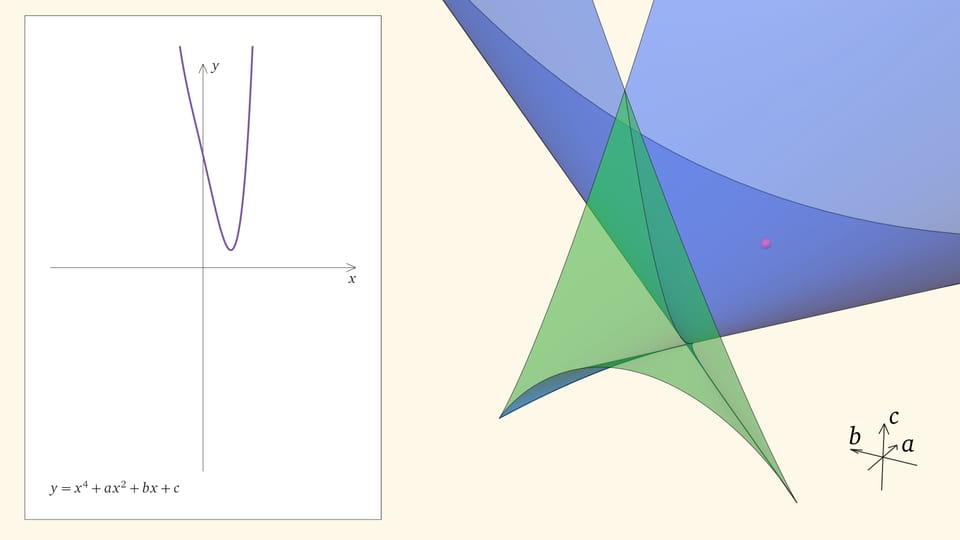
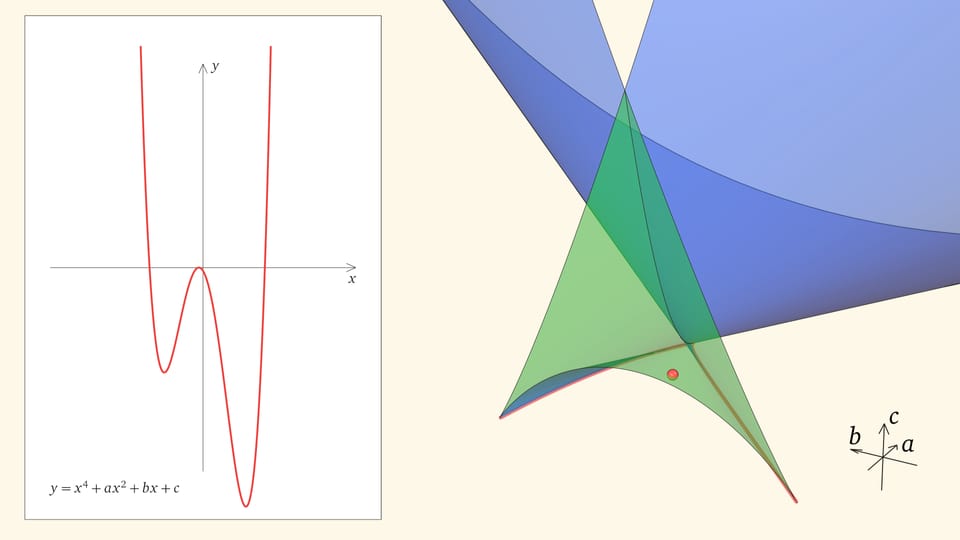
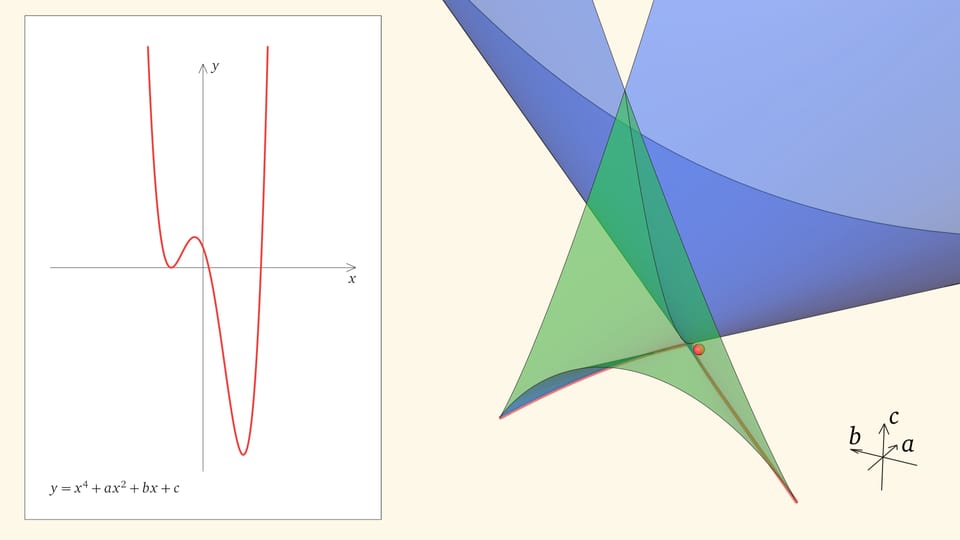
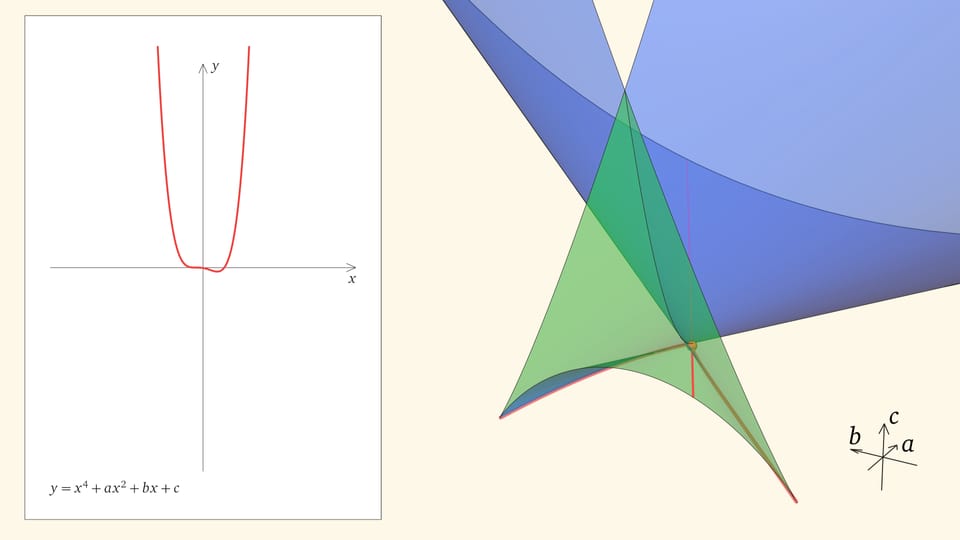
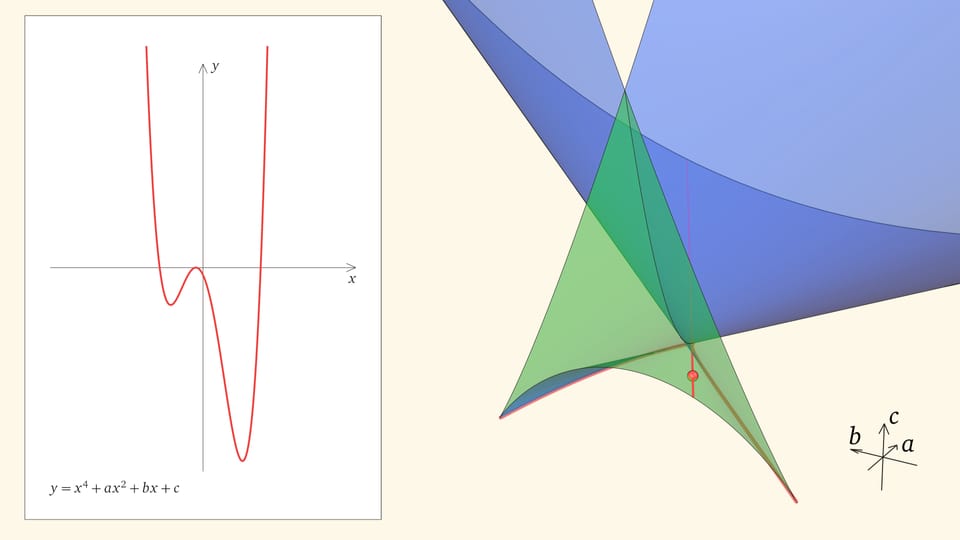
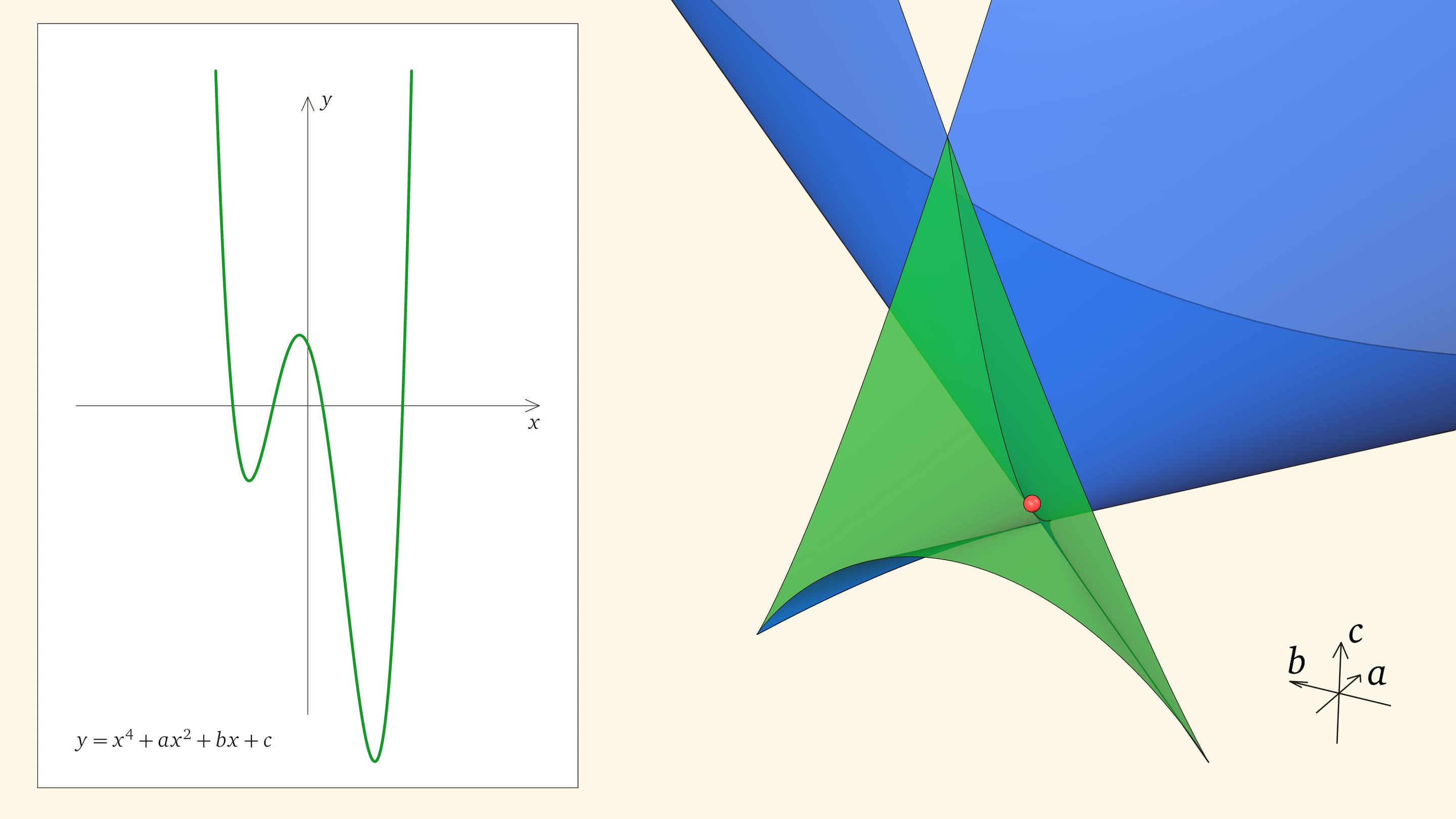
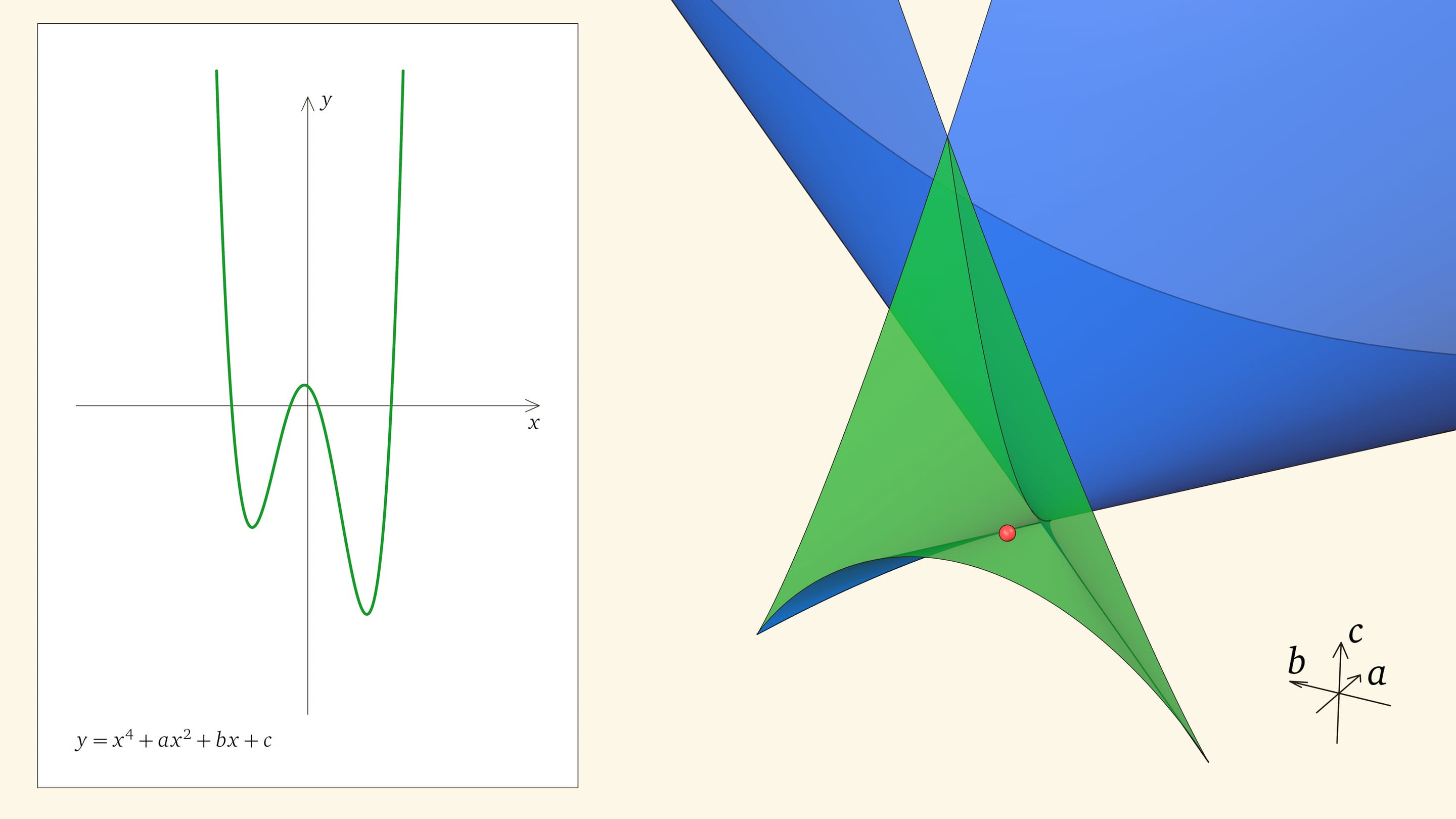
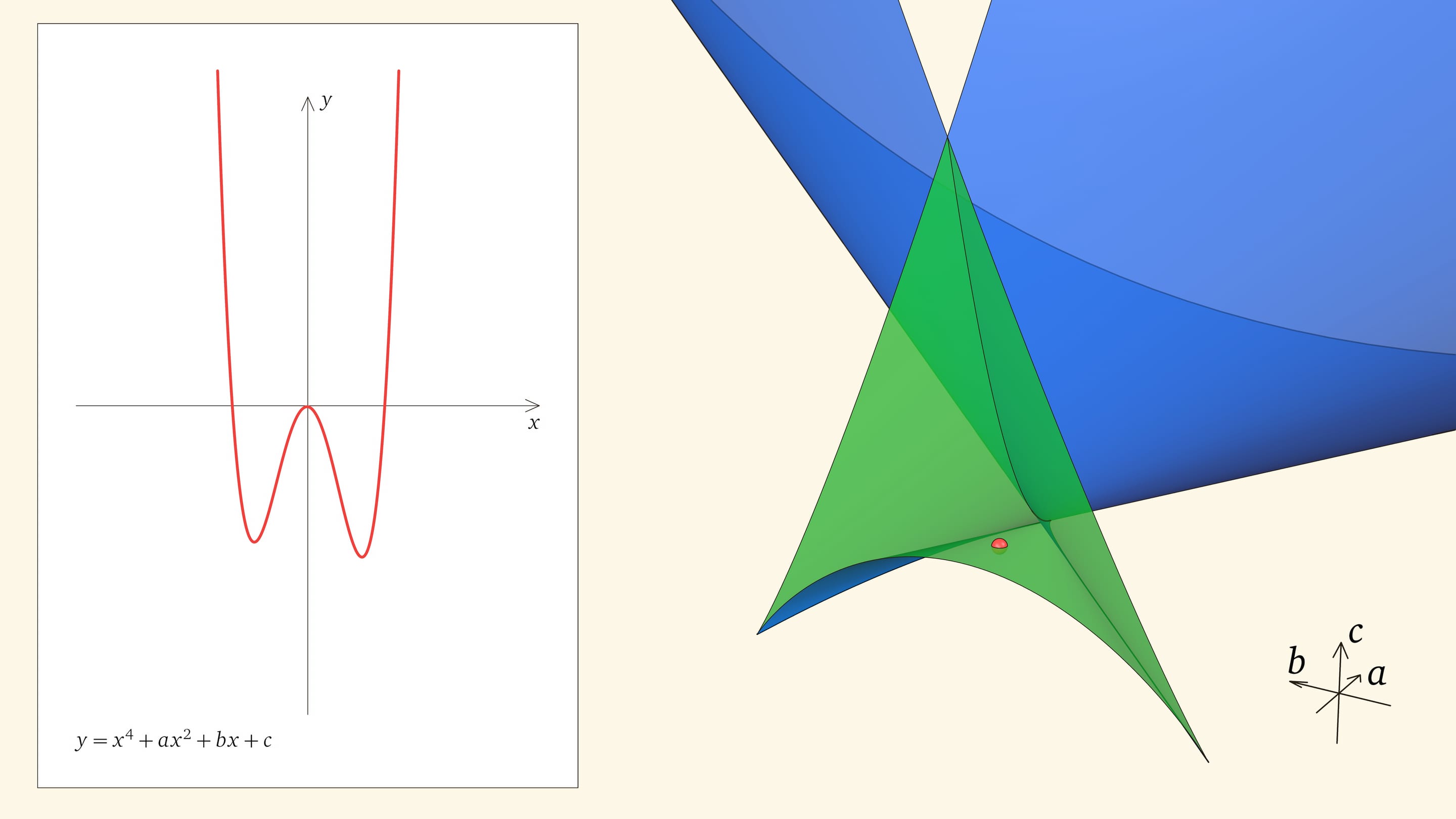
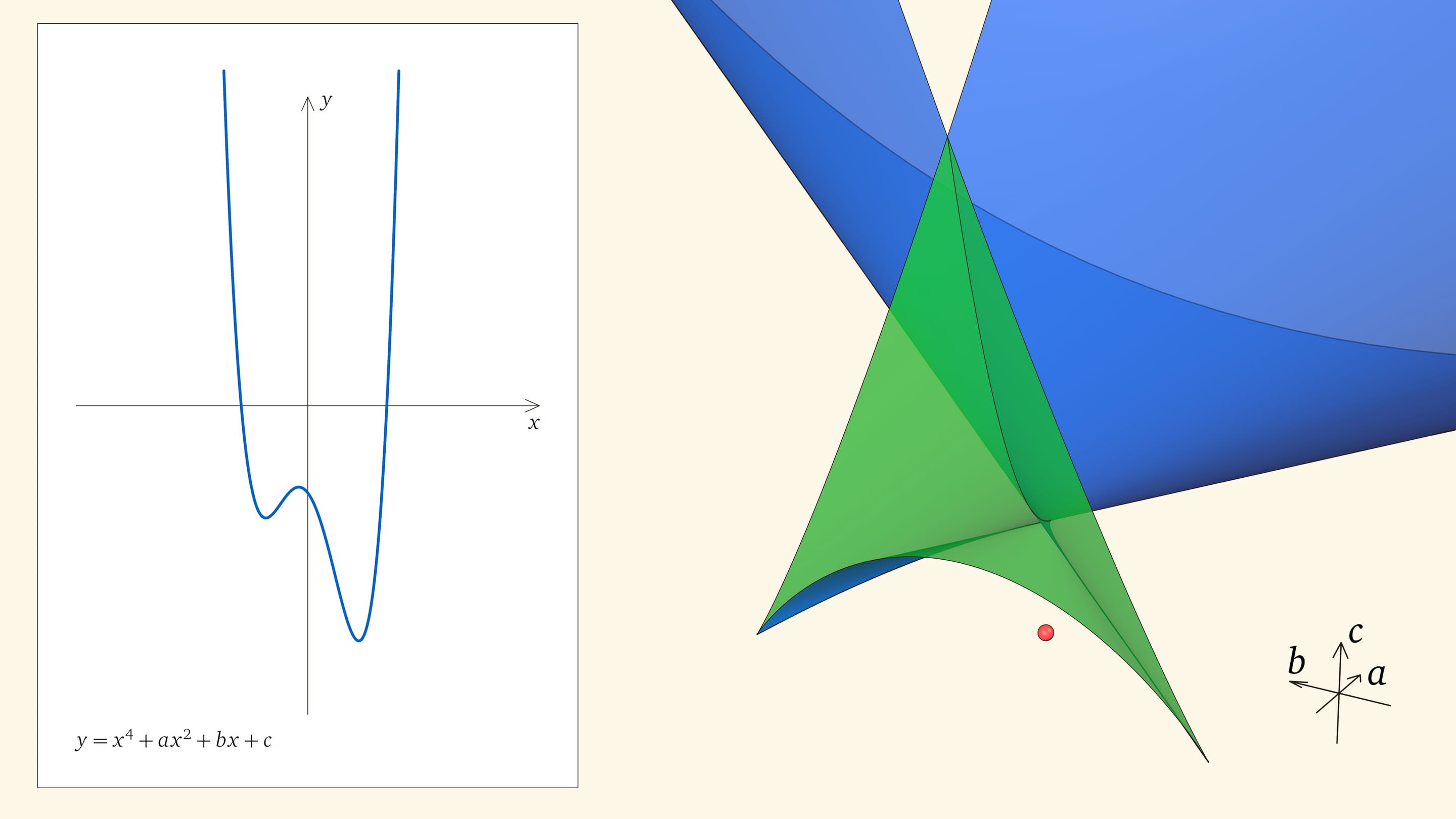
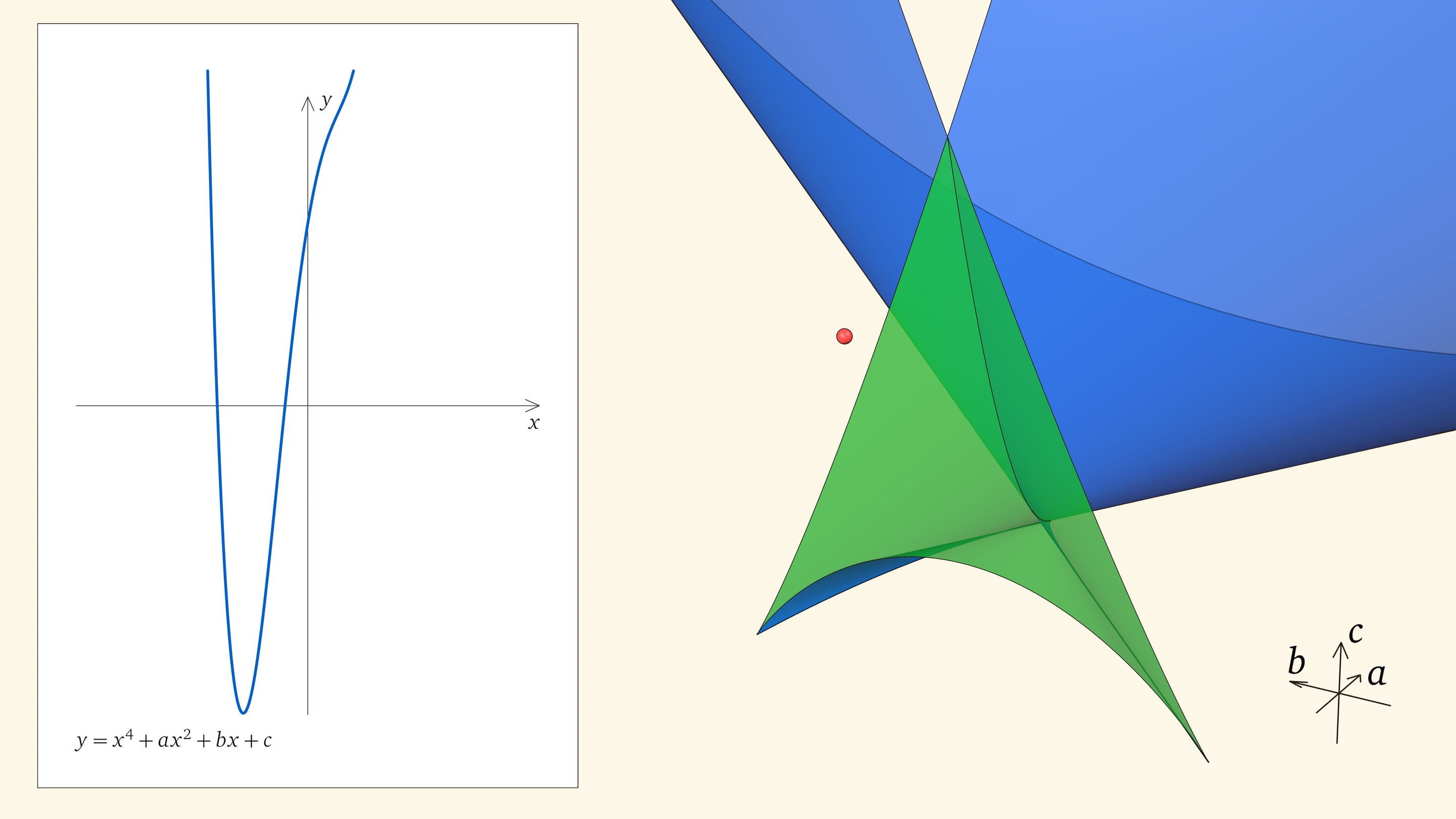
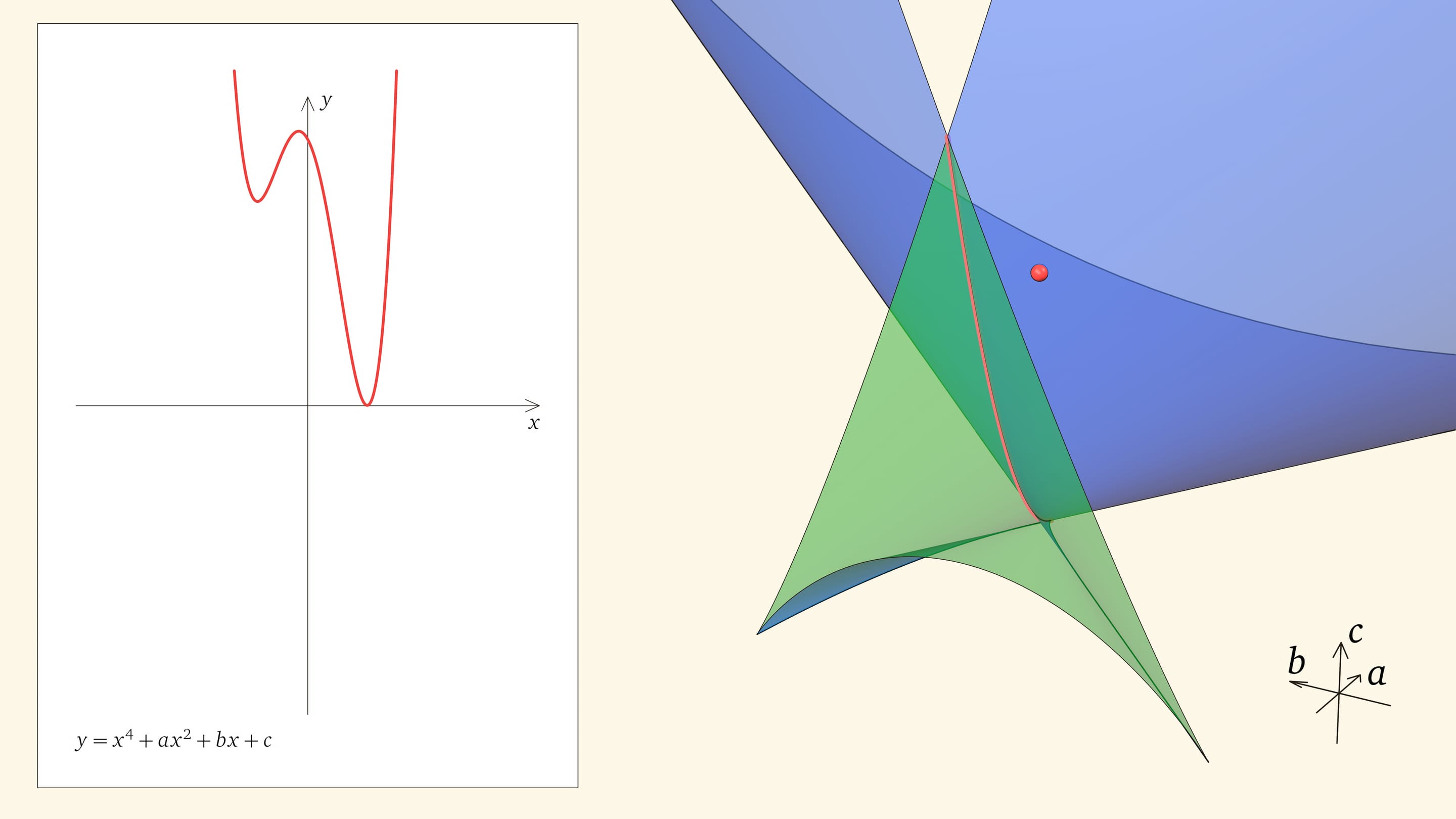
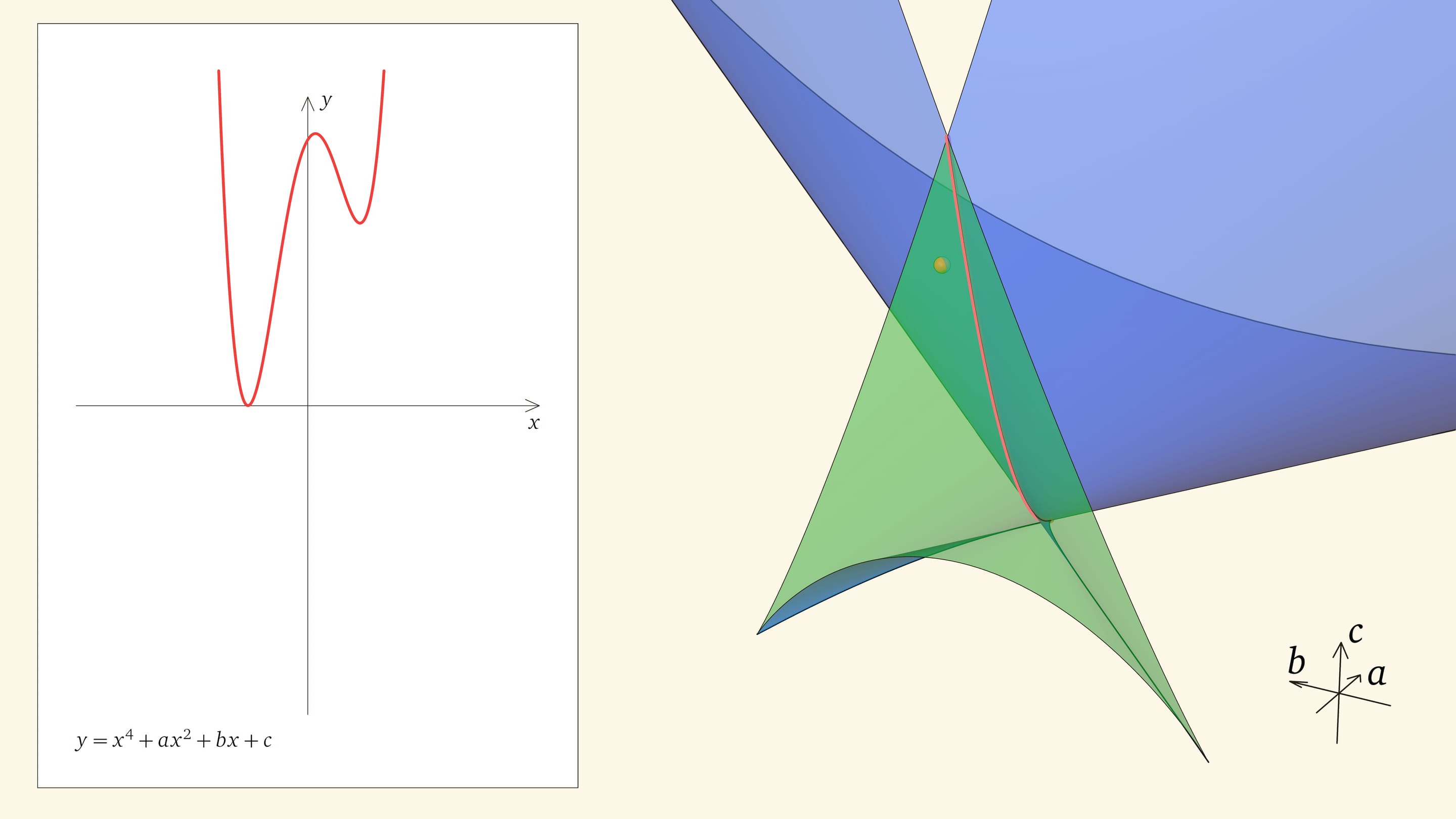
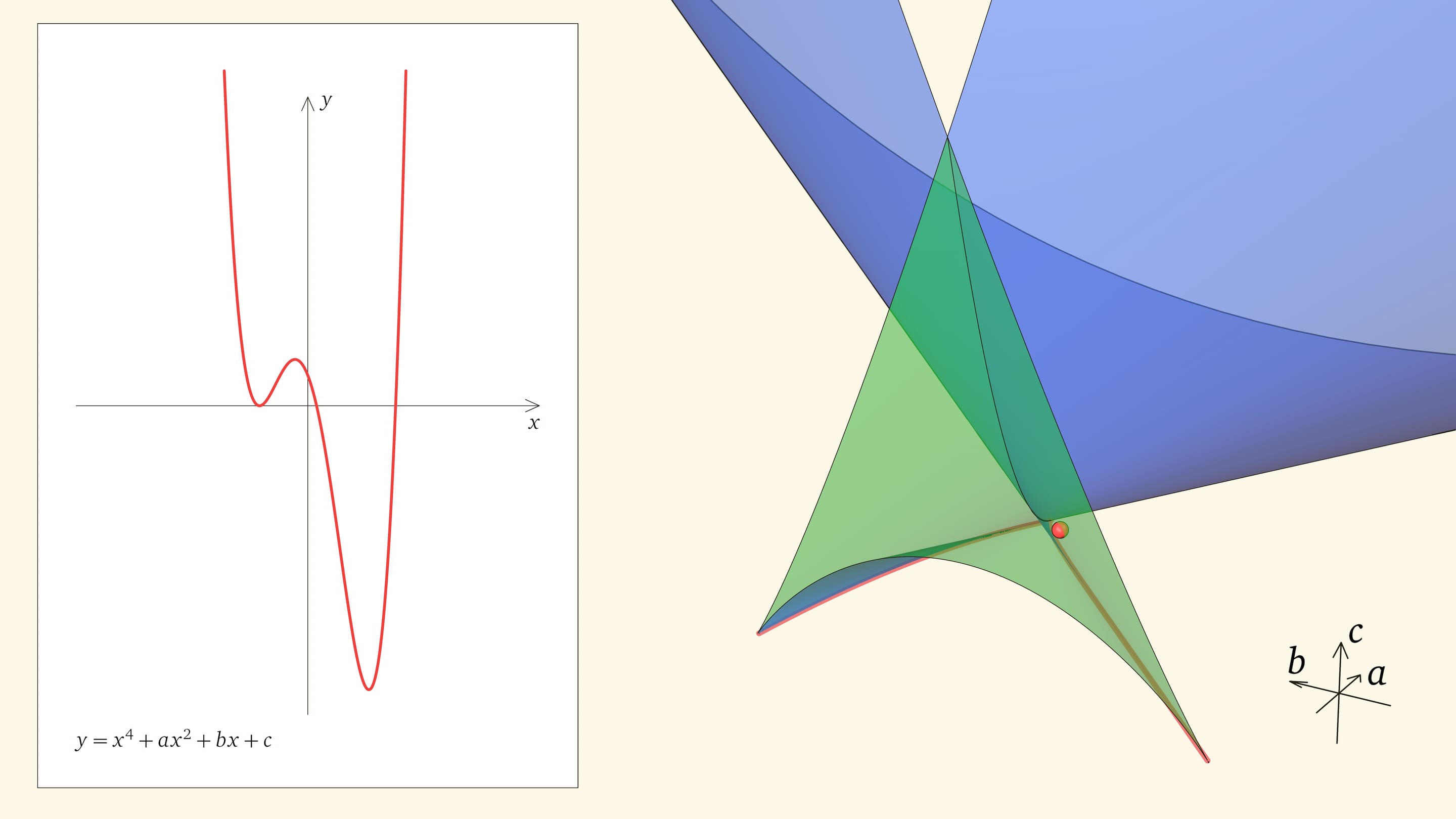
Посмотрим на количество точек пересечения графика функции $y=x^4+ax^2+bx+c$ с осью $Ox$ — количество корней уравнения — в зависимости от положения точки $(a,b,c)$ относительно дискриминантной поверхности в пространстве параметров.
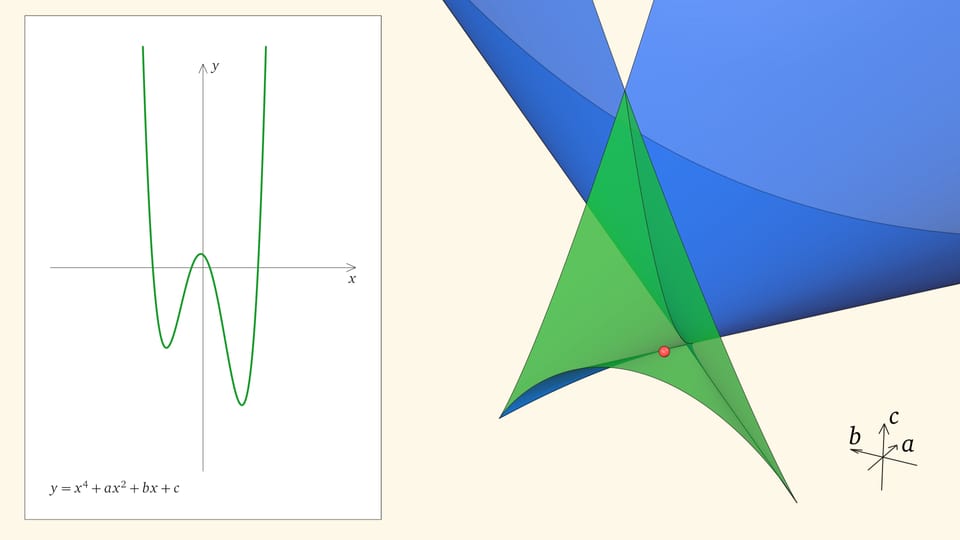
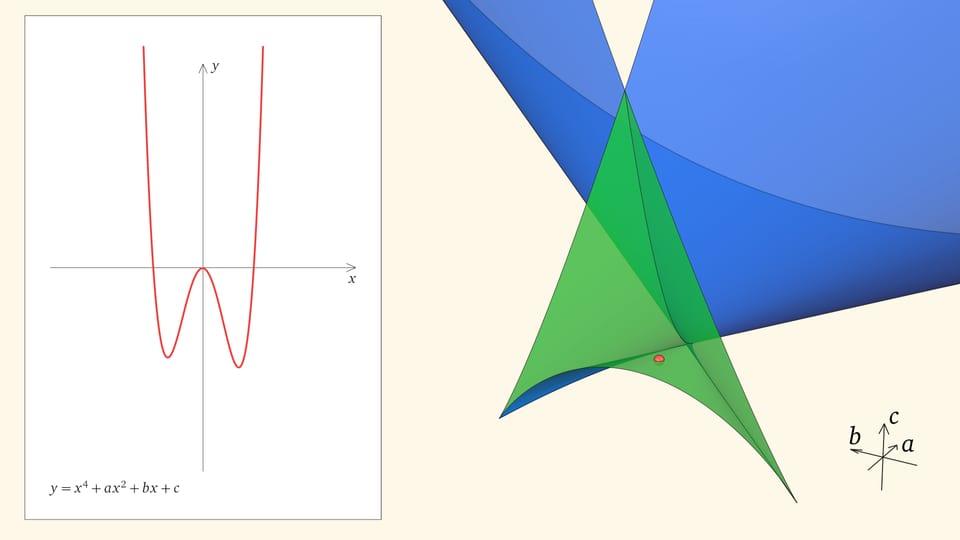
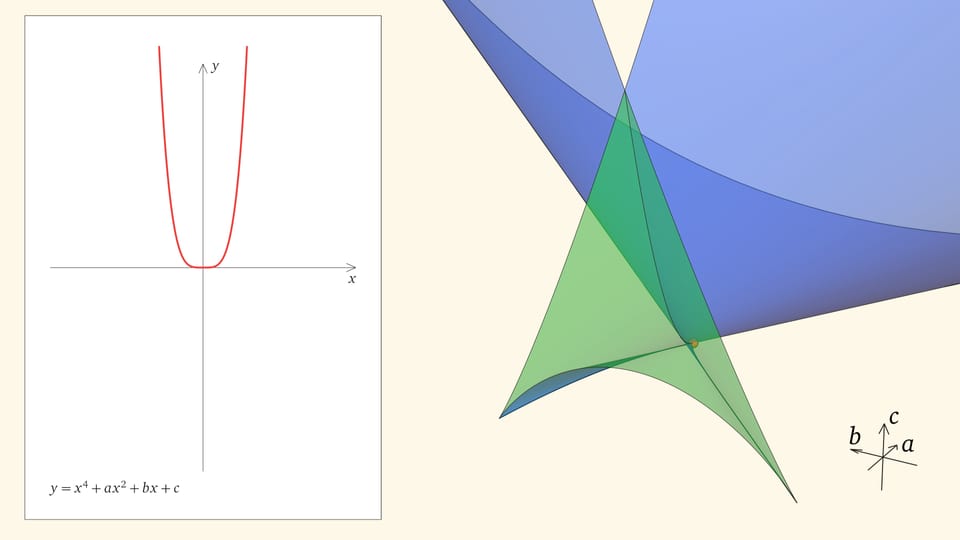
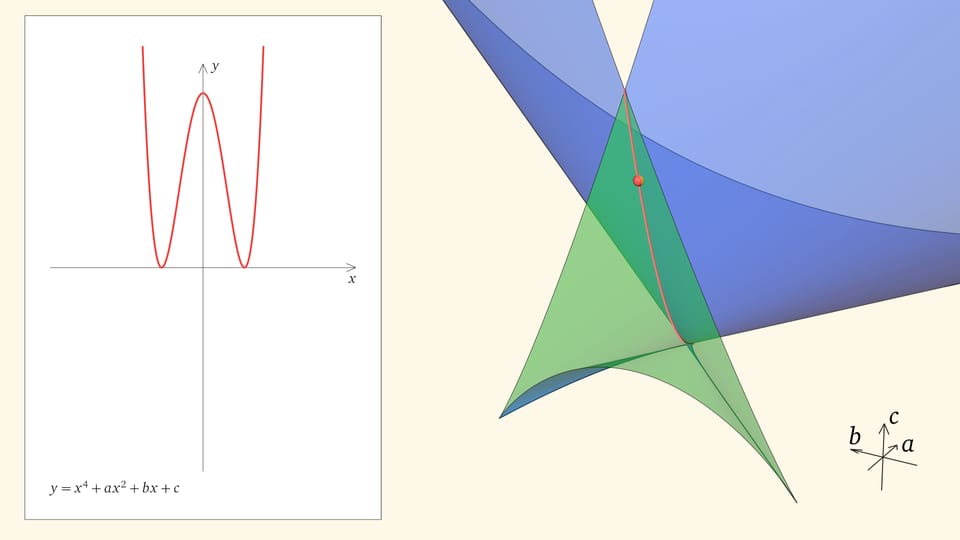
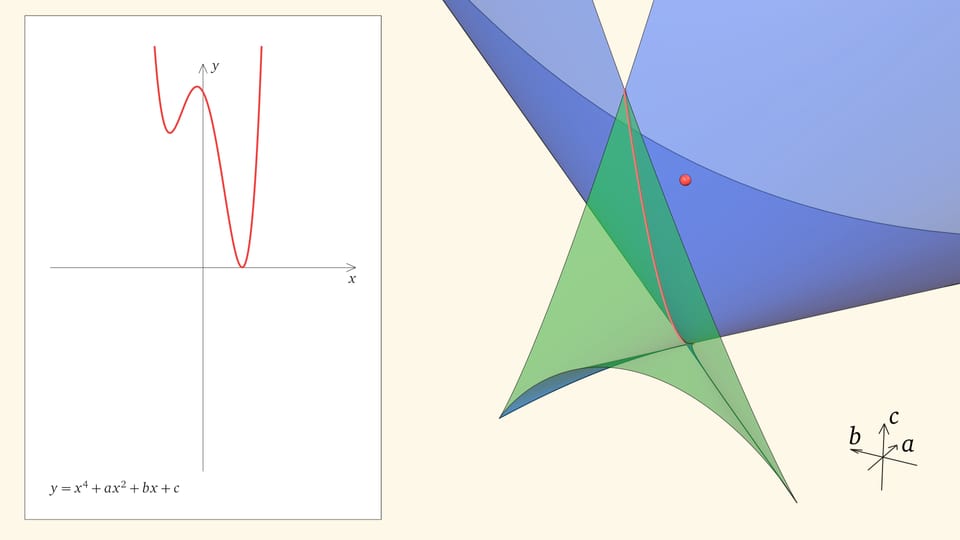
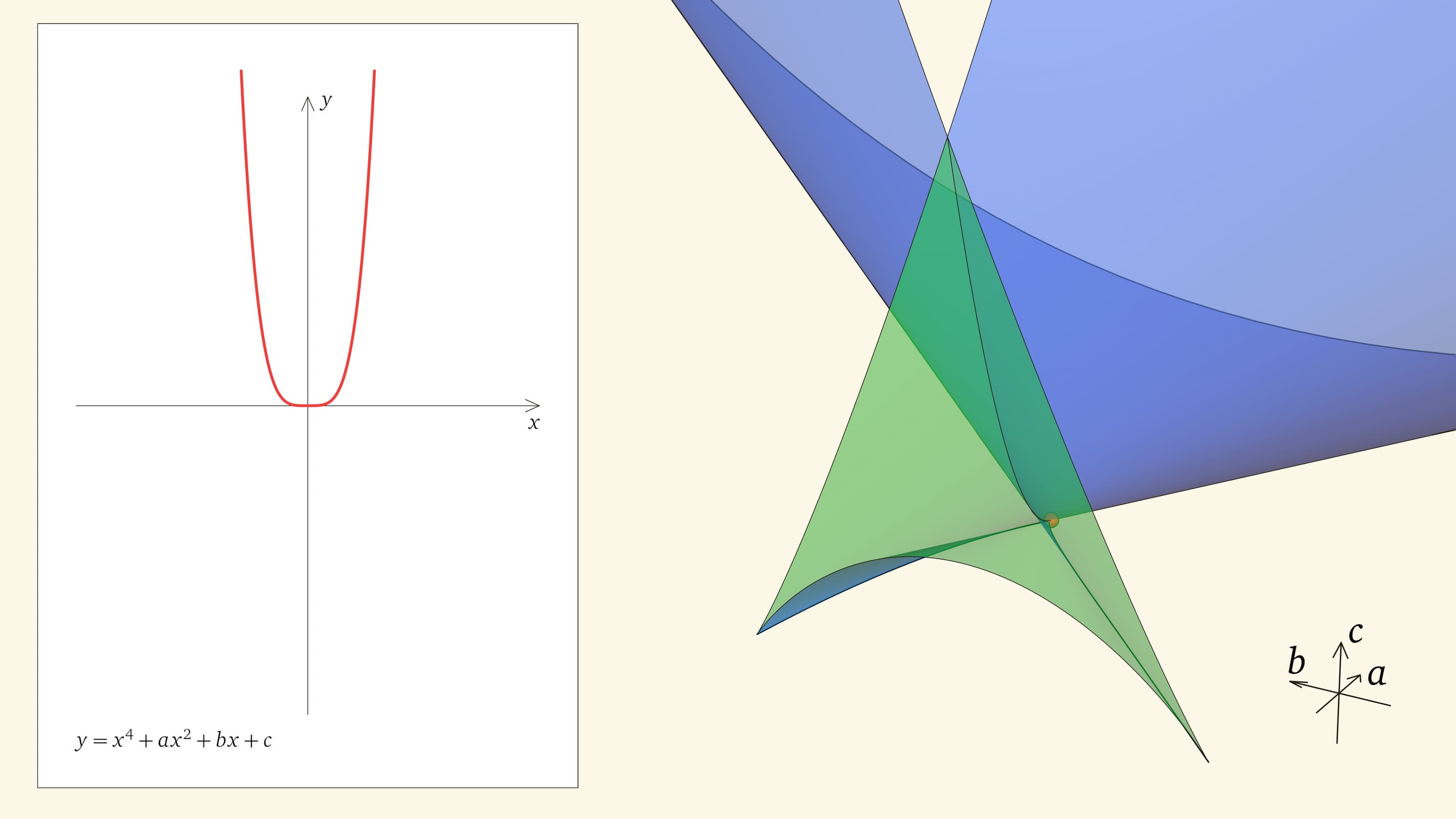
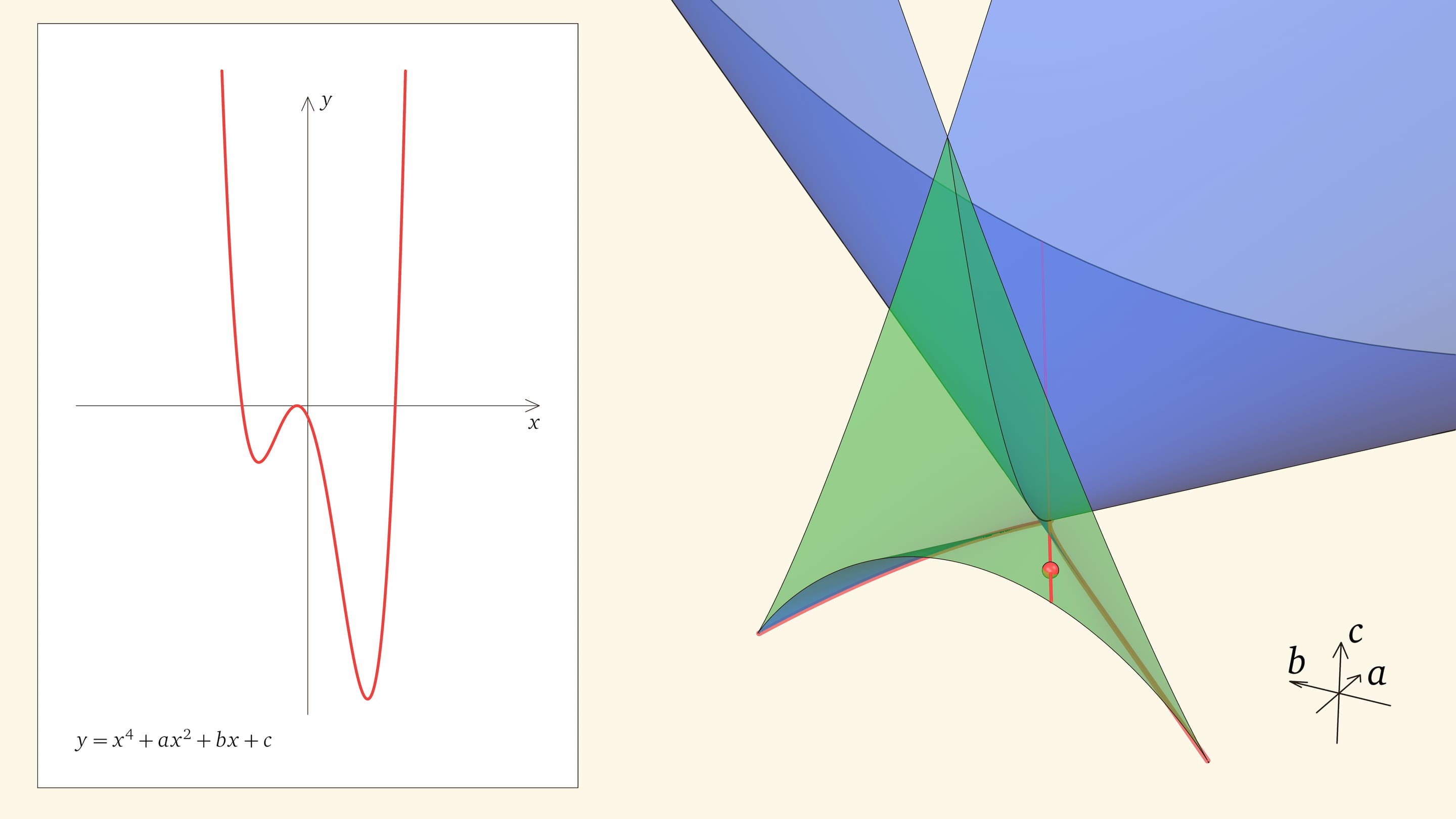
Если точка лежит в зелёной области — внутри криволинейного угла, — то функция имеет четыре нуля, т. е. уравнение $x^4+ax^2+bx+c=0$ имеет четыре действительных корня. Для перехода из зелёной области в синюю необходимо пересечь дискриминантную поверхность, и в момент пересечения «грани угла» два нуля из четырёх сливаются.
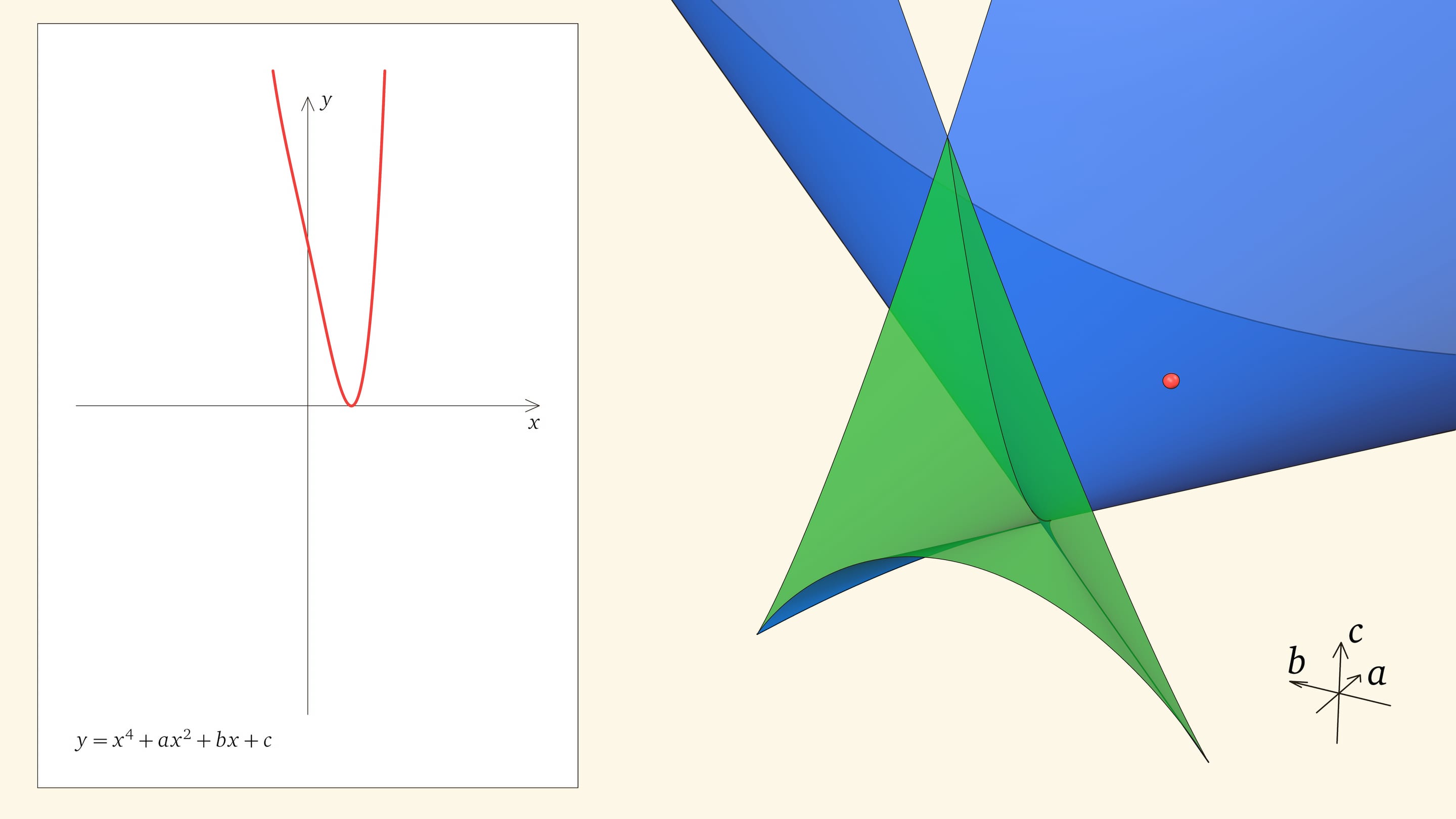
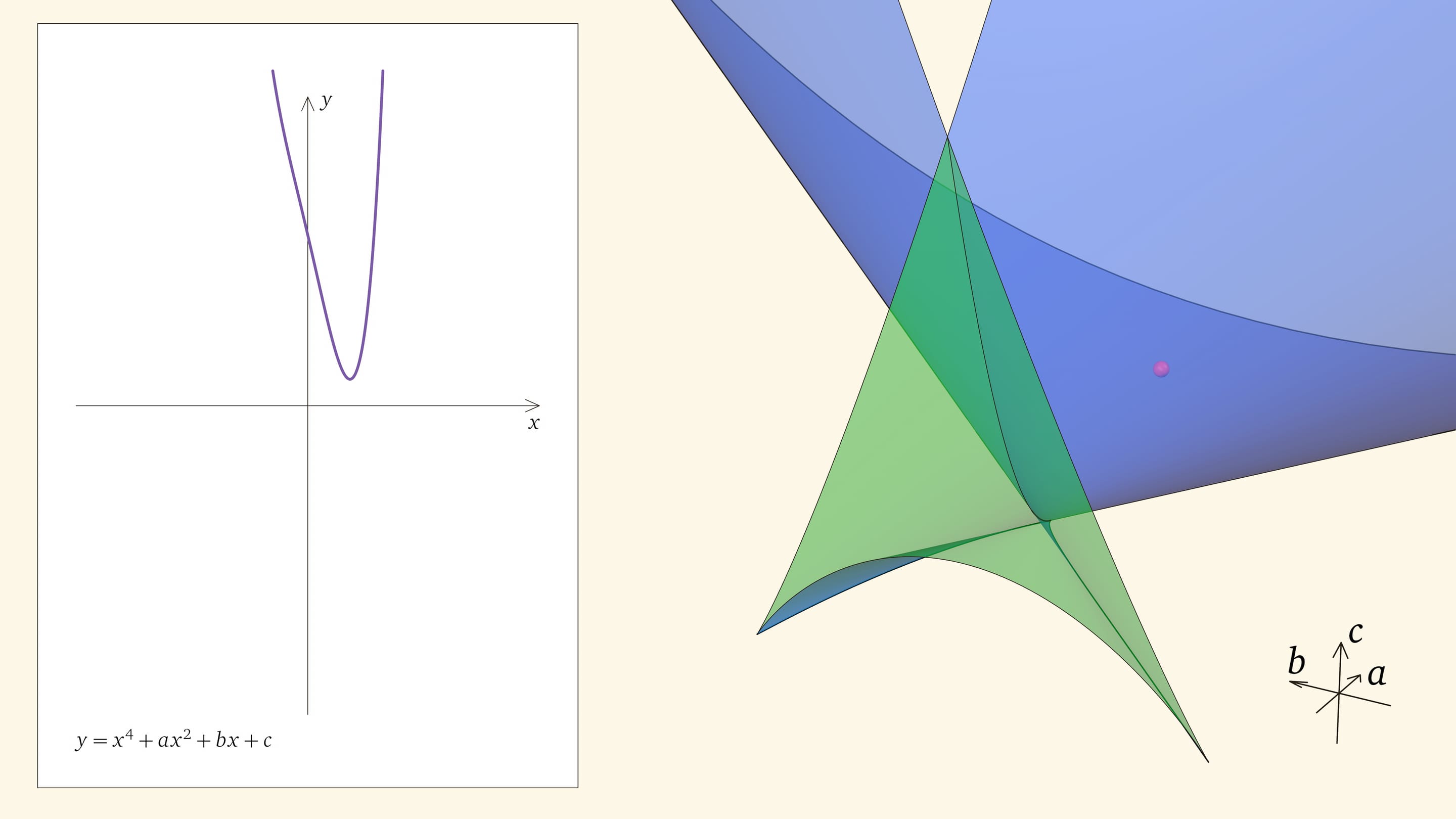
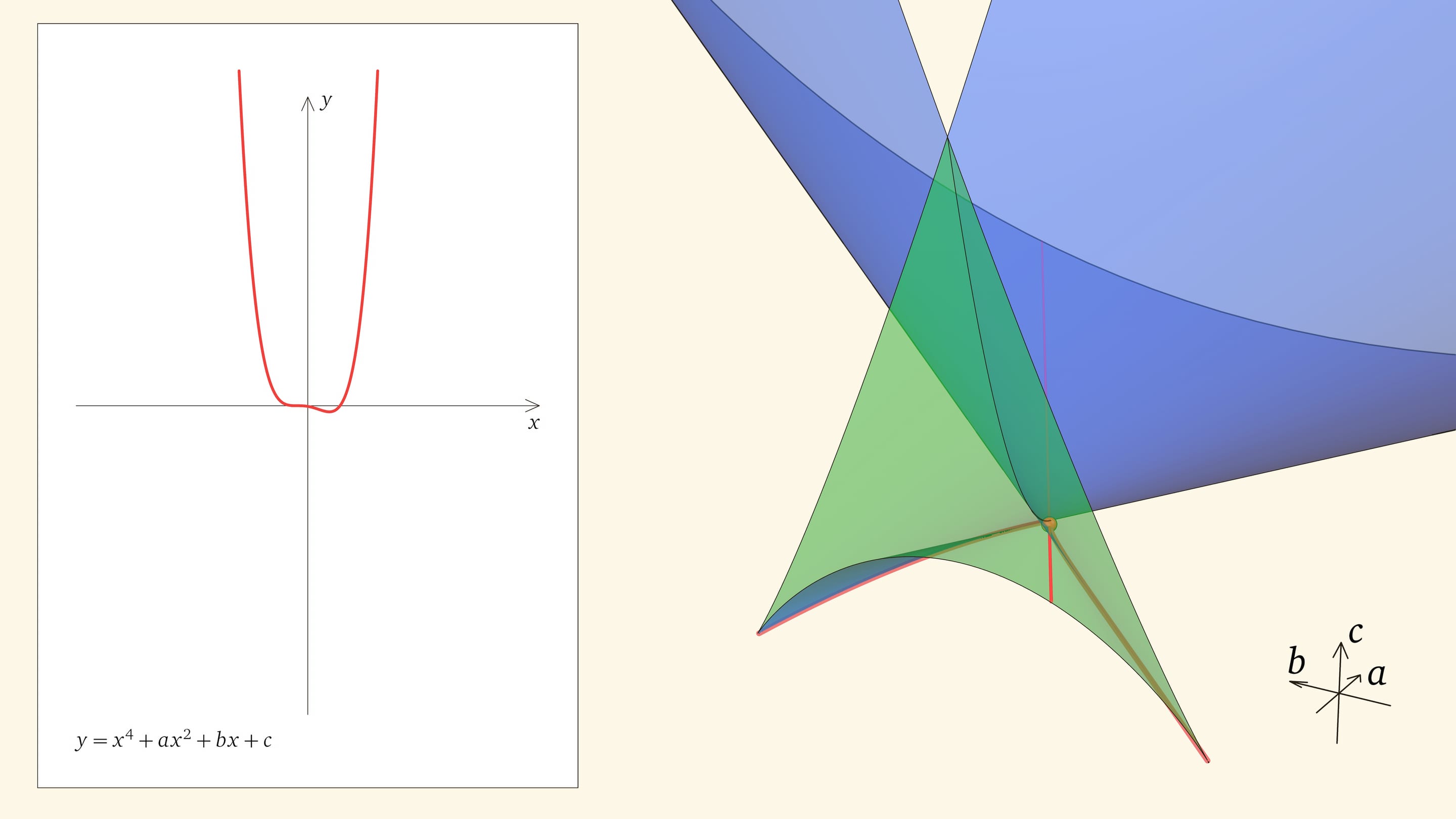
Нахождение точки в синей области — под дискриминантной поверхностью и вне зелёной области — отвечает уравнениям с двумя действительными корнями. На границе синей и фиолетовой областей сливаются и эти два корня.
При нахождении точки в фиолетовой области — над ласточкиным хвостом — у соответствующего уравнения действительных корней нет.
Вершиной ласточкиного хвоста является точка $(0,0,0)$, отвечающая функции $y=x^4$, у которой один ноль четвёртого порядка.
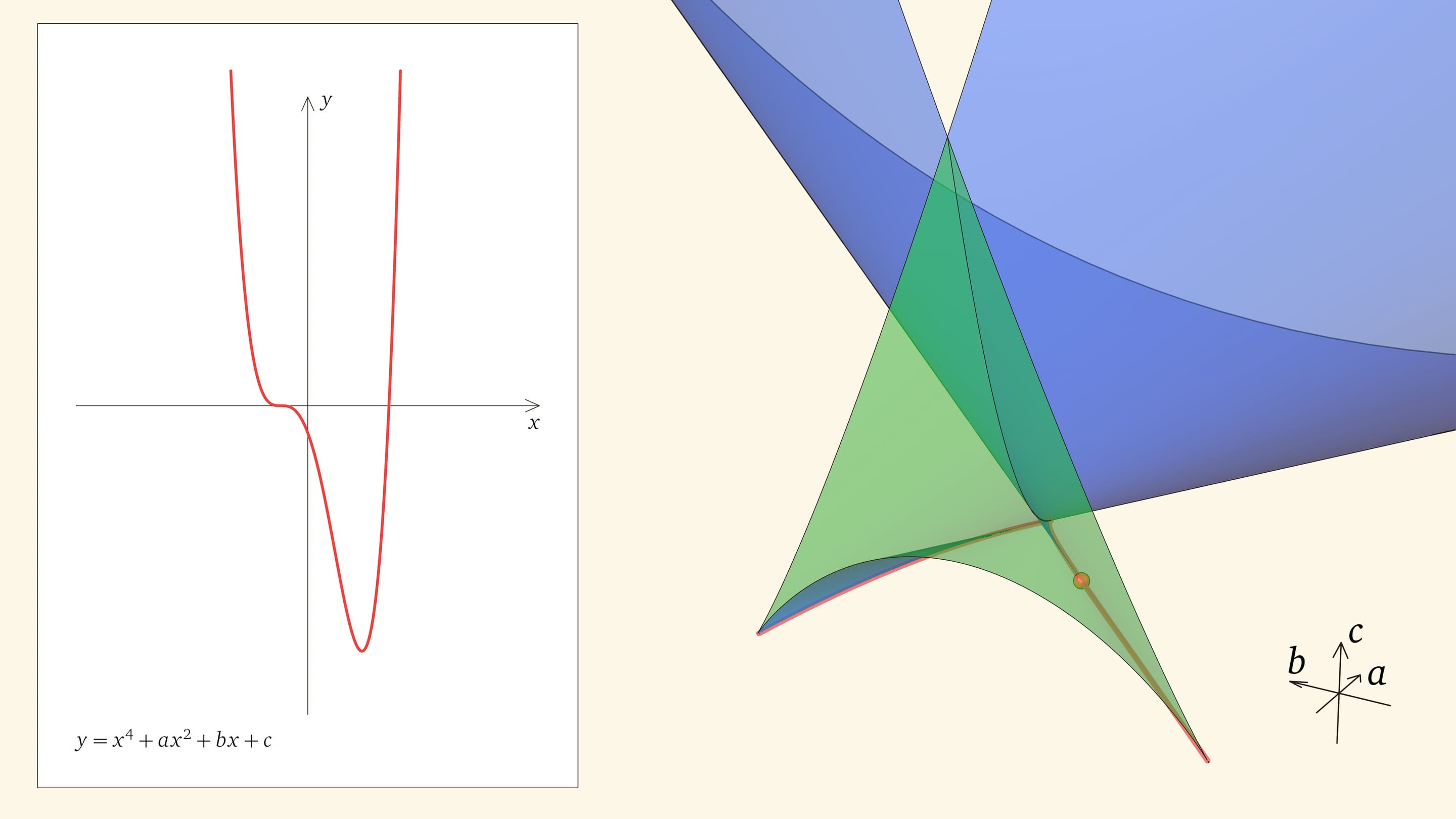
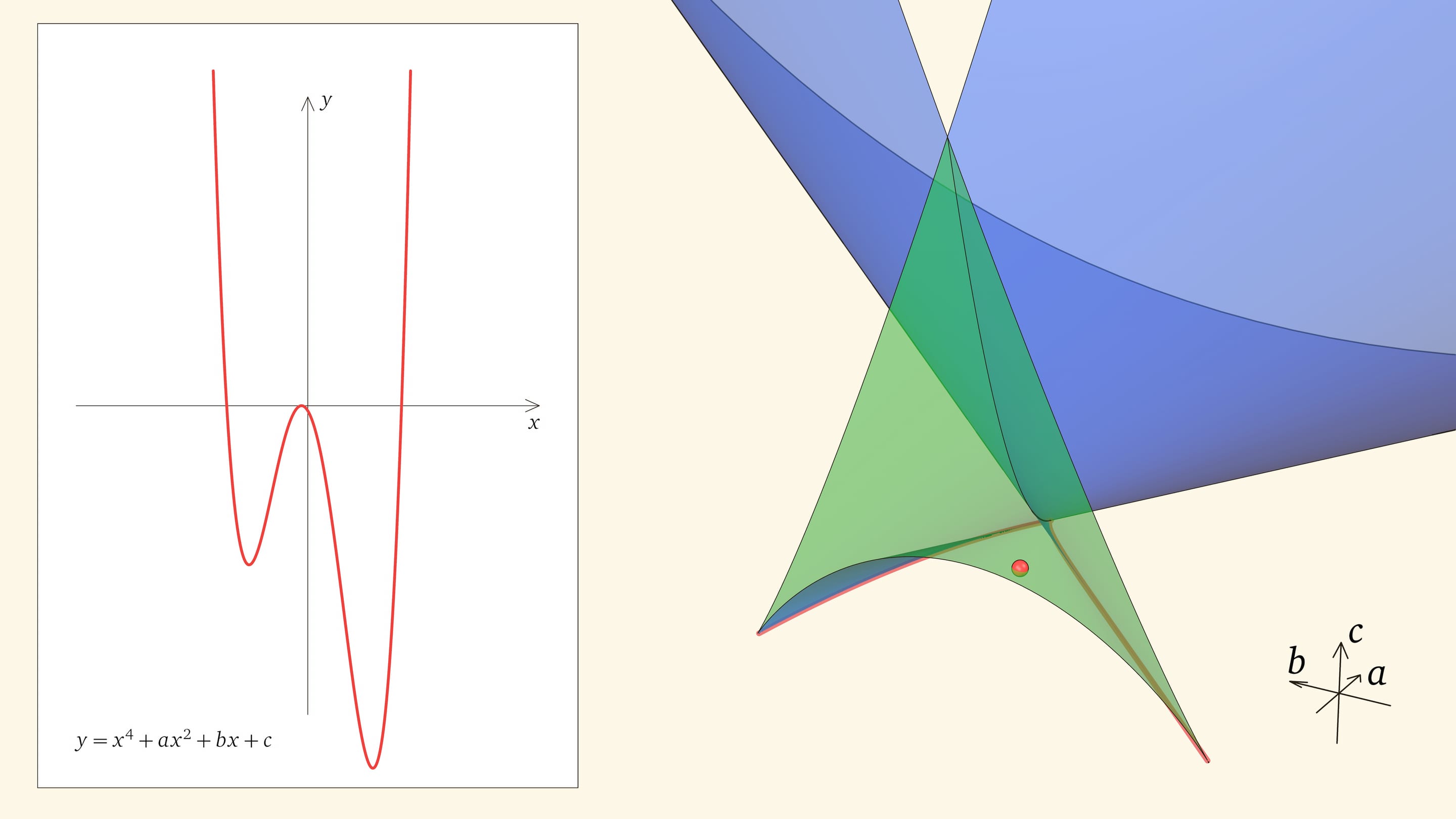
Линия самопересечения дискриминантной поверхности, выходящая из вершины вверх, отвечает многочленам, имеющим два двойных корня. Если от линии самопересечения уйти, оставаясь на дискриминантной поверхности, в одну сторону, то у уравнения будет один двойной корень, если в другую, — корень будет тоже двойной, но другого знака. Соответственно, на линии самопересечения два симметричных относительно нуля двойных корня; она соответствует функциям вида $y=(x^2+\alpha)^2$ при $\alpha\le 0$.
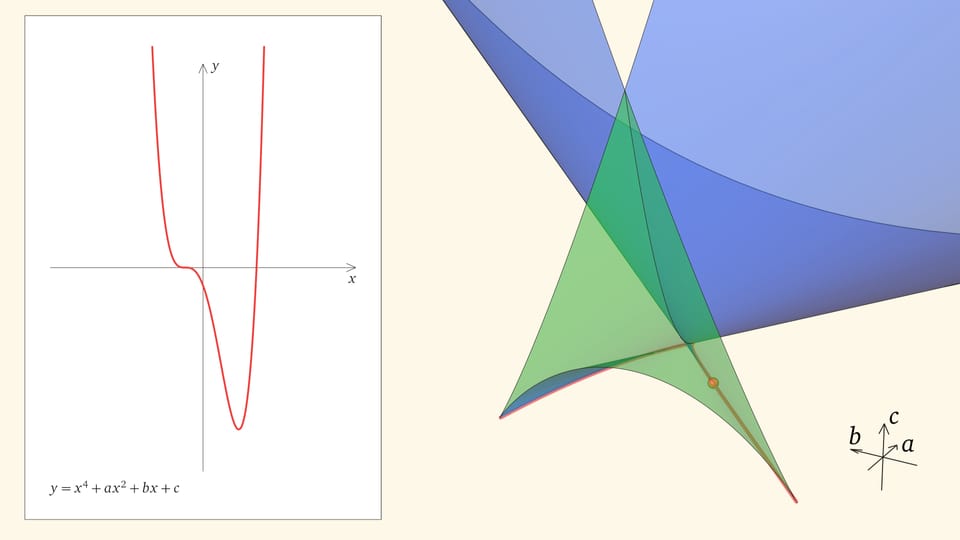
Ребро возврата соответствует многочленам с одним тройным корнем и одним простым. Действительно, если выйти внутрь зелёного угла, то корней, как мы помним, четыре. Когда точка приходит на нижнюю грань угла, из этих четырёх корней сливаются два средних. Когда точка находится на боковой грани угла, то сливаются крайние два корня (с какой стороны — зависит от того, на какой из боковых граней находится точка). На общем для боковой и нижней гранях ребре возврата сливаются три корня из четырёх. На другой половинке ребра сливаются три корня с другой стороны.
Как уже было показано, прямолинейные образующие дискриминантной поверхности касаются ребра возврата. Точки, лежащие на прямолинейной образующей, отвечают многочленам с одним общим фиксированным корнем. Когда точка находится на участке прямой, отвечающем зелёному углу, — это один из трёх корней, когда в основной части ласточкиного хвоста — единственный.
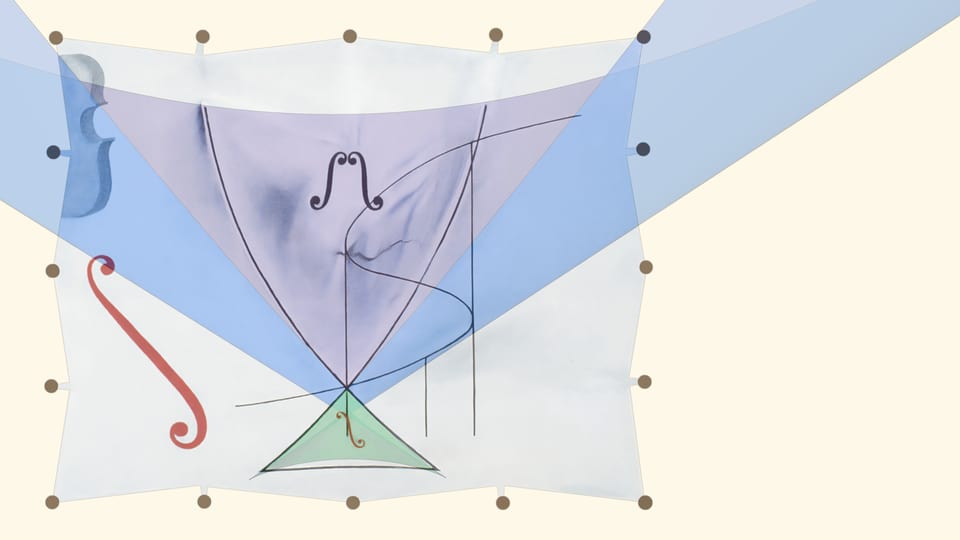
Дискриминантная поверхность уравнений четвёртой степени «ласточкин хвост» стала героем последней написанной маслом работы Сальвадора Дали. На ней также изображена $S$-образная кривая, символизирующая ещё одного представителя теории особенностей — сборку. Картина завершает серию «Теория катастроф» из четырёх работ знаменитого испанца.
По некоторым источникам, Сальвадор Дали рисовал кривую по графику Рене Тома. Мы не смогли подобрать сечение ласточкиного хвоста, совпадающее с кривой Дали. Возможно, дело в том, что ласточкиным хвостом называют не только дискриминантную поверхность уравнений четвёртой степени, но и просто особенность такого вида (когда взгляд чисто топологический).
Рене Том (René Frédéric Thom, 1923—2002) получил в 1958 году медаль Филдса за создание теории кобордизмов. Впоследствии занялся теорией катастроф — областью, объединяющей важный раздел математики «теорию особенностей» и приложения этой теории к объяснению явлений окружающего нас мира. В 60—70-х годах XX века теория катастроф была чрезмерно популярна. Состоялась встреча Рене Тома и Сальвадора Дали, оказавшая на испанца большое влияние. Даже в своей ответной речи «Гала, Веласкес и Золотое руно», будучи выбранным в иностранные члены Академии изящных искусств (Académie des beaux-arts) Института Франции 24 мая 1978 года, Сальвадор Дали упоминал и Рене Тома, и теорию катастроф.
Серия «Теория катастроф» Сальвадора Дали (1983):
- «Топологическое похищение Европы. Посвящение Рене Тому», внизу нарисован ласточкин хвост и выписан многочлен, чья производная является многочленом четвёртой степени без кубического члена;
- без названия;
- без названия, «Ласточкин хвост и виолончели»;
- без названия, «Ласточкин хвост».
По некоторым источникам, Дали оформил множеством рисунков (а книжная графика у Дали богатейшая) работу Тома «Параболы и катастрофы. Беседы о математике, науке и философии».
Как вспоминал Том, «Не знаю, с чего вдруг я удостоился такой чести. Дали я видел не более пяти минут, и к тому же давным-давно. Мне сказали, что его последняя картина «Топологическое похищение Европы» посвящена моим работам. Думаю, дело скорее в навязчивых идеях мэтра, именно им я обязан запоздалым и чрезмерным энтузиазмом по поводу моих исследований, давно уже известных среди учёных».
Леопольд Кронекер, автор знаменитой фразы «Бог создал целые числа, всё остальное — дело рук человеческих» (Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk) в статье 1878 года аналитически, не рисуя графиков, полностью исследовал дискриминантную поверхность уравнений четвёртой степени. Для интересующихся напишем некоторые формулы и мы.
Для уравнений любой степени, а не только квадратных, можно написать дискриминант — многочлен от коэффициентов уравнения, равный нулю тогда и только тогда, когда уравнение имеет кратные корни (не обязательно действительные). Для уравнений $x^4+ax^2+bx+c=0$ дискриминант имеет вид $$ \Delta=16a^4c-4a^3b^2-128a^2c^2+144ab^2c-27b^4+256c^3. $$
Понять, как устроена поверхность $\Delta=0$ в пространстве $Oabc$, не так уж просто.
Другой подход к построению дискриминантной поверхности использует свойства кратного корня. В момент, когда два корня сливаются и у уравнения появляется кратный корень, график касается оси $Ox$. В точке касания $t$ обращается в ноль не только сам многочлен, но и его производная: $$ \begin{cases} t^4+at^2+bt+c=0{,} \\ 4t^3+2at+b=0.\end{cases} $$
Выражая $b$ и $c$ через значение кратного корня $t$ и коэффициент $a$, получаем параметрическое задание дискриминантной поверхности: $b=-4t^3-2at$ (из второго уравнения), $c=3t^4+at^2$. (Рост ласточкиного хвоста в начале фильма и то, как он «обрезан», соответствуют некоторым значениям параметров $t$ и $a$.)
Отметим, что если $t$ фиксировано, то $b$ и $c$ зависят от $a$ линейно. То есть множество всех уравнений с данным кратным корнем $t$ представляется в пространстве параметров прямой, а вся дискриминантная поверхность является объединением таких прямых. Каждая из этих прямых касается ребра возврата: точка касания соответствует единственному уравнению, для которого $t$ не просто кратный, а трёхкратный корень. Коэффициенты уравнения $x^4+ax^2+bx+c=0$, соответствующие точке касания, легко найти по теореме Виета: так как три корня равны $t$, $t$, $t$, то оставшийся четвёртый корень равен $-3t$ (сумма корней равна минус коэффициенту при $x^3$, то есть нулю), а для остальных коэффициентов получаем $a=-6t^2$, $b=-8t^3$, $c=-3t^4$.
Как отмечалось, это даёт ещё один способ построить ласточкин хвост: рассмотреть поверхность, состоящую из всех касательных к ребру возврата — кривой $(-6t^2,-8t^3,-3t^4)$.
Построенная таким образом поверхность не совсем совпадает с поверхностью $\Delta=0$. Дело тут в многочленах вида $(x^2+\alpha)^2$ для $\alpha\gt 0$. У них вещественных корней нет, а есть две пары кратных комплексных корней. Поверхность $\Delta=0$ такие уравнения включает по определению дискриминанта, а вот рассмотренная параметризация их не учитывала. Геометрически такие уравнения соответствуют кривой, продолжающей линию самопересечения ласточкиного хвоста (соответствующую уравнениям $(x^2+\alpha)^2$ для $\alpha \le 0$) в фиолетовую область симметрично за вершину.
Литература
Васильев В. А. Геометрия дискриминанта. — М.: МЦНМО, 2017. — (Библиотека «Математическое просвещение»; Вып. 41).
Клейн Ф. Элементарная математика с точки зрения высшей. Т. 1: Арифметика, алгебра, анализ. — 4-е изд. — М.: Физматлит, 1987. — С. 137—147. — [Первое издание на русском: Клейн Ф. Вопросы элементарной и высшей математики. — Одесса: Mathesis, 1912. — С. 154—166].
Арнольд В. И. Теория катастроф. — 3-е изд., доп. — М.: Наука, 1990.
Kronecker L. Über Sturmsche Functionen // Monatsberichte der Königlicli Preussischen Akademie der Wissenschaften zu Berlin. — Feb. 1878. — P. 95—121.