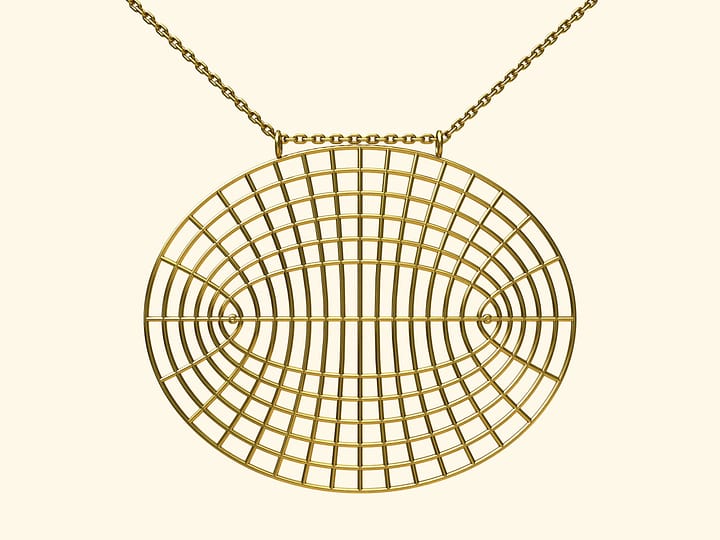
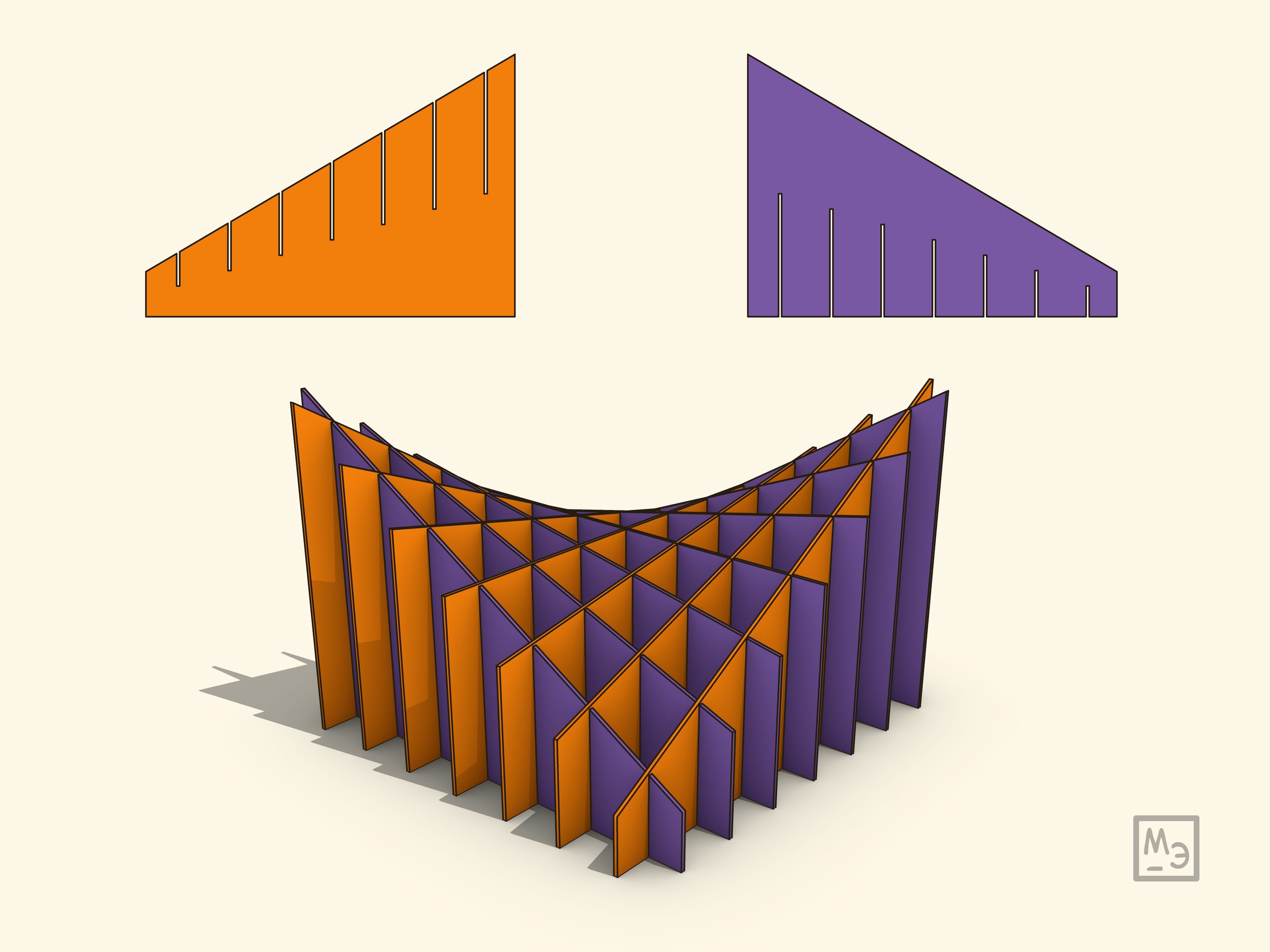
Картонная модель гиперболического параболоида удивительна. В её названии участвуют слова, изучаемые только в старших классах школы (и то по отдельности, а вместе — уже только в университете). Она позволяет явно увидеть нетривиальные свойства этой сложной поверхности. При этом сделать и обсудить такую модель можно даже с детьми.
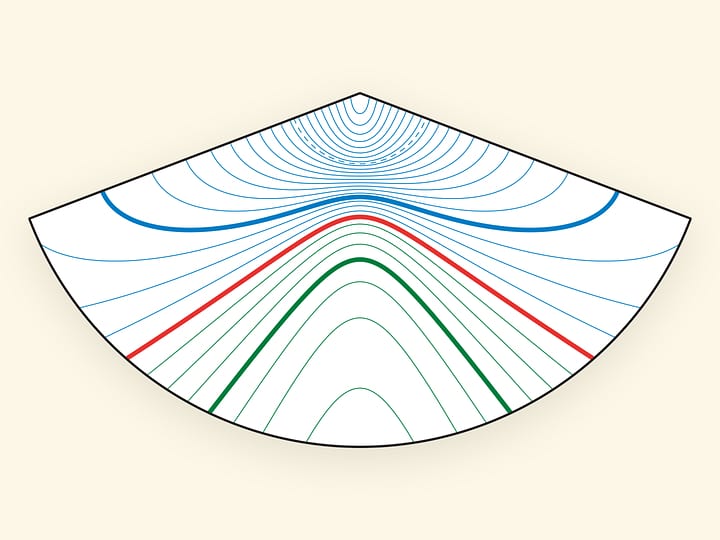
Увидеть анимированное определение гиперболического параболоида, разобраться, где там параболы, а где гиперболы, можно, посмотрев фильм Седловидная поверхность: гиперболический параболоид. А свойство линейчатости этой седловидной поверхности — то, что она образована движением прямой линии — можно продемонстрировать проделав противоречащий интуиции эксперимент с чипсами, показанный в фильме Чипсы: гиперболический параболоид.
Картонная модель позволяет ещё более наглядно убедиться в свойстве линейчатости гиперболического параболоида — она явно предъявляет образующие из обоих семейств. Опять же явно картонная модель позволяет убедиться и в том, что поверхность гиперболического параболоида «не плоская» (имеет отрицательную гауссову кривизну) — листочек бумаги нельзя не помяв уложить на неё.
Рассматриваемая модель гиперболического параболоида является изгибаемой: её можно сжимать, сохраняя параллельность картонок в каждом из двух семейств, но меняя угол между этими семействами. При этом точки пересечения образующих, очевидно, будут неизменны, сама поверхность будет меняться, но всегда оставаться гиперболическим параболоидом. Случай прямого угла соответствует «школьным» прямоугольным гиперболам, когда их асимптоты перпендикулярны. Теоретически, можно было бы сделать такую книгу-панораму (Pop Up), но если использовать негнущийся (соответственно, относительно толстый) картон, то количество слоёв слишком велико, чтобы она хорошо закрывалась «в плоскость».
«На заметку»: порядок слов в названии «гиперболический параболоид» можно запомнить по первым буквам слов — они идут в алфавитном порядке, как в русском, так и в английском алфавитах.
Литература
Гиперболический параболоид // Журнал «Квант». — 1990. — № 3. — Стр. обл. 1, 4.
Чипсы // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 90.