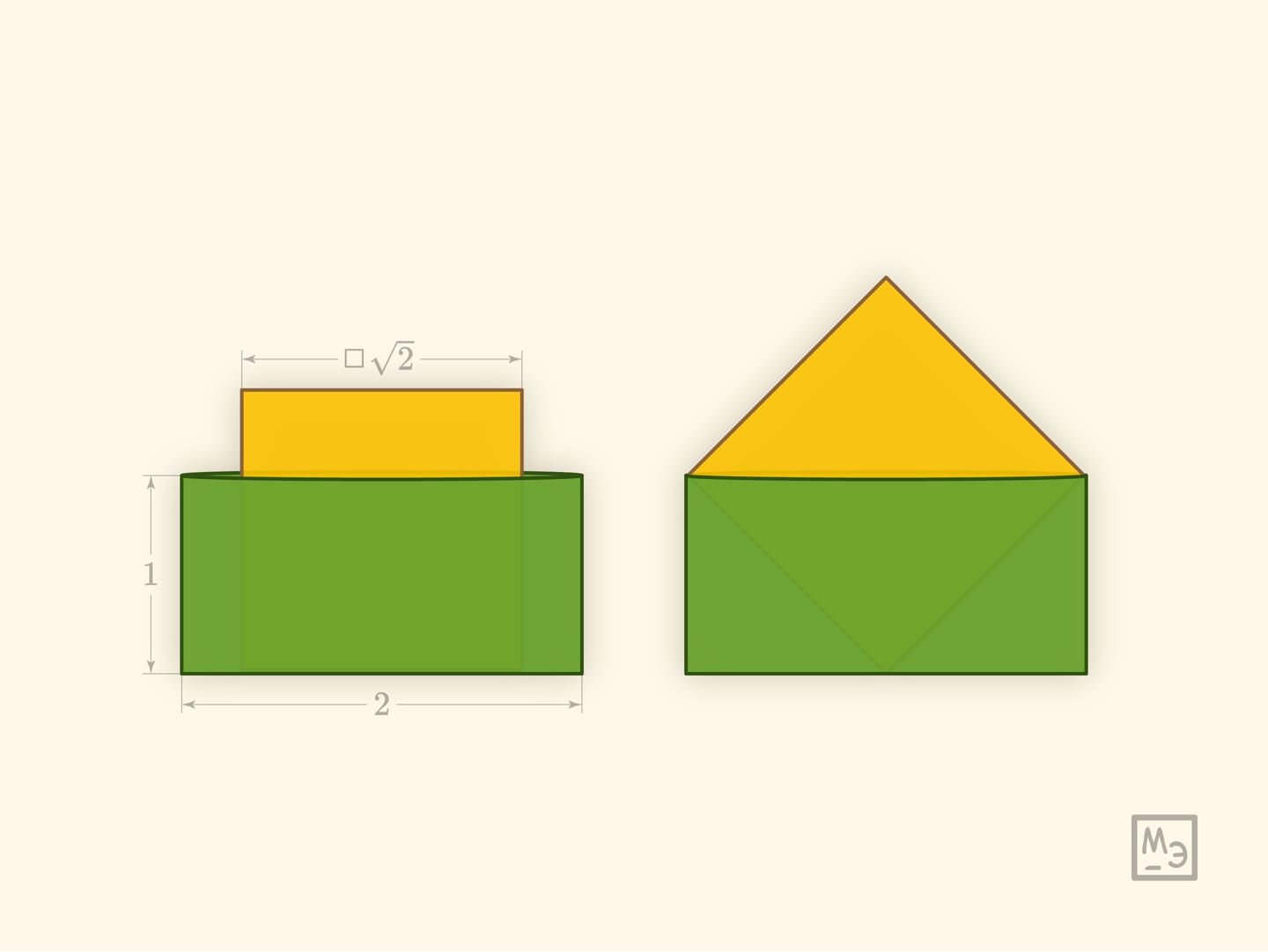
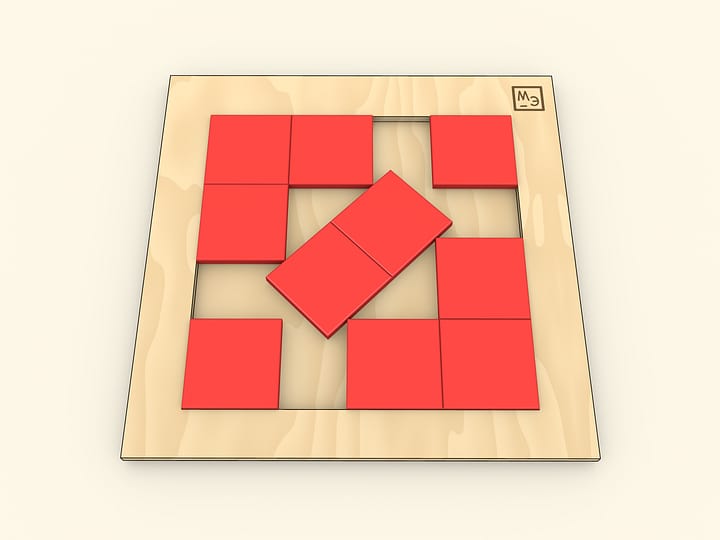
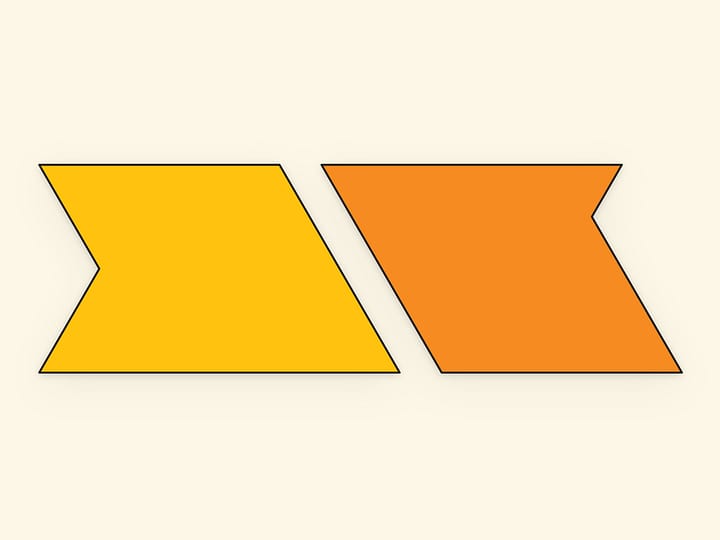
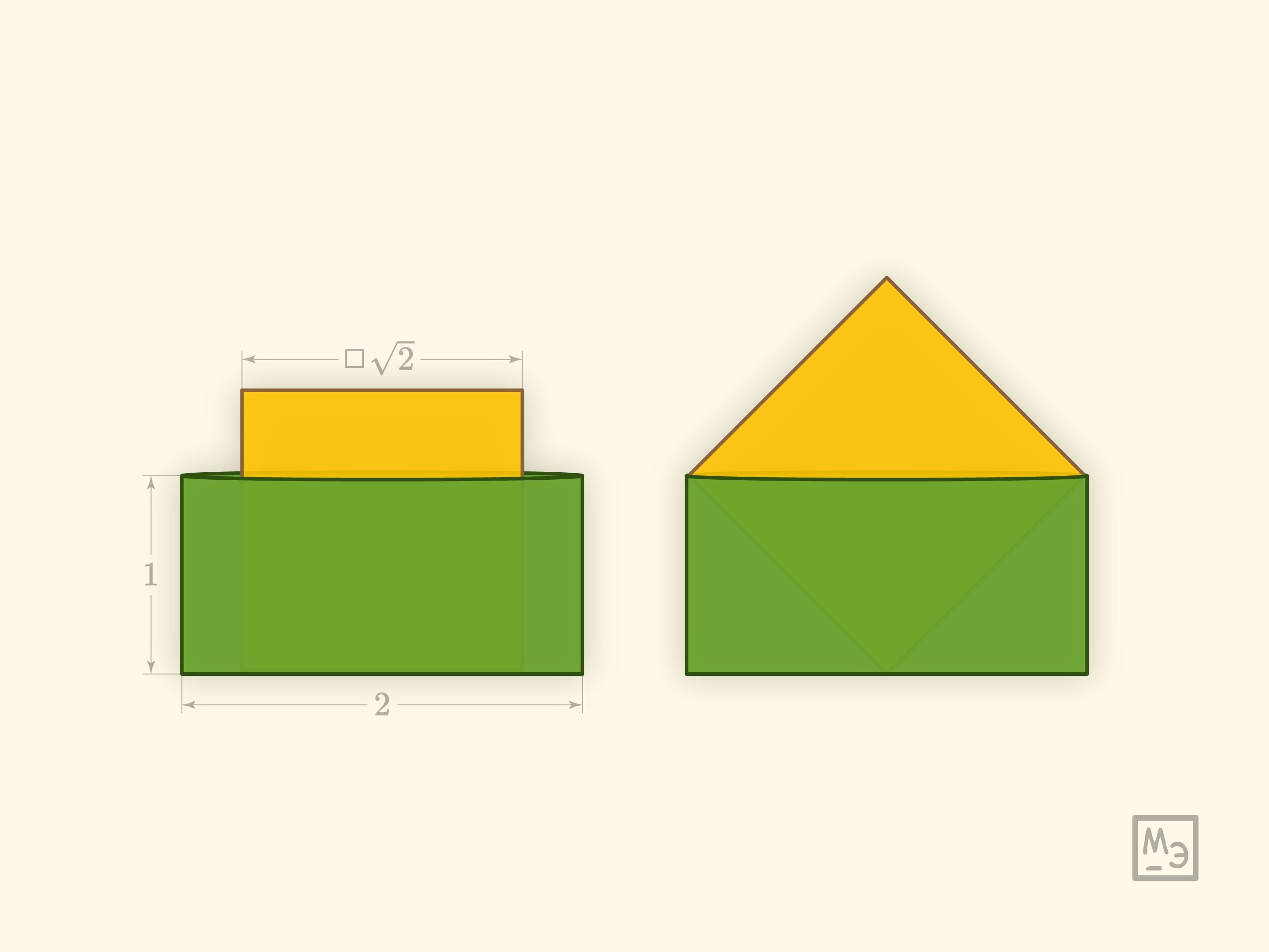
Квадрат со стороной $\sqrt{2}$ требуется уложить в прямоугольный мешочек со сторонами $2$ и $1$. Удивительно, но эта изящная, простая по постановке и реализации головоломка, была придумана совсем недавно, уже в XXI веке. Её автор — Hirokazu Iwasawa (Iwahiro), а сама головоломка была признана лучшей головоломкой 2012 года и удостоена Puzzlers’ Award.
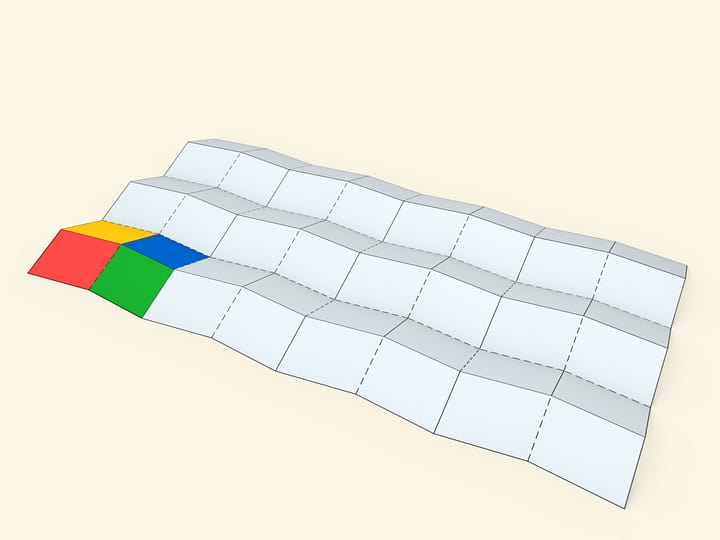
Довольно быстро приходит понимание конечного положения мешочка: как он будет сложен, чтобы покрывать квадрат с обеих сторон. Но как поместить квадрат внутрь? И вот тут помогает геометрия.
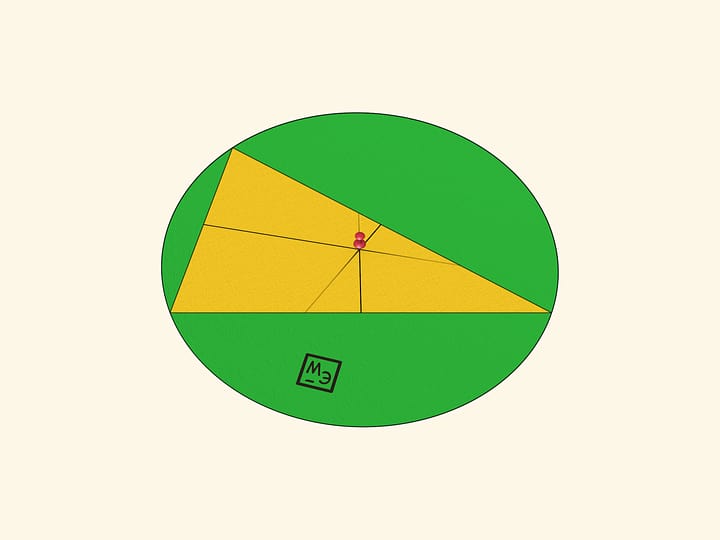
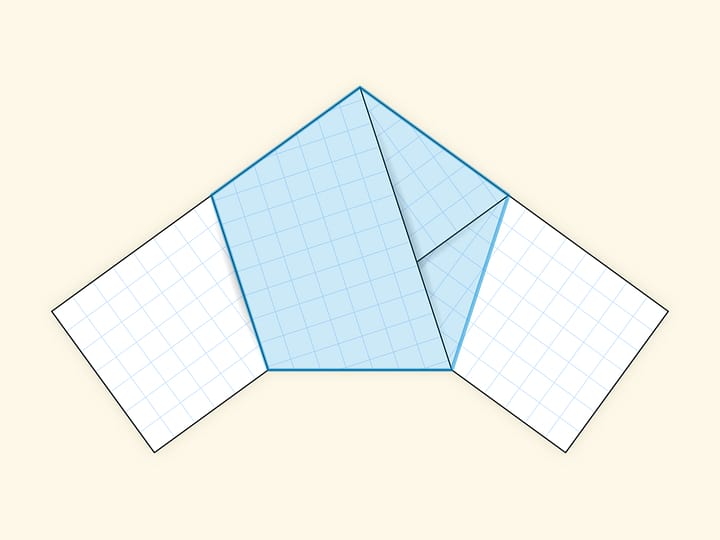
Мешочек следует натягивать на противоположные углы квадрата, надвигая его на равные расстояния. Край мешочка всегда будет натянут — образовывать прямоугольник. Две противоположные стороны этого прямоугольника, параллельные одной из диагоналей квадрата, «охватывают» квадрат сверху, а другие две, параллельные другой диагонали, — снизу. Нетрудно убедиться, что периметры всех таких прямоугольников одинаковы! Это и позволяет полностью засунуть квадрат в мешочек.
Головоломка может быть использована как «мерч» — и на квадрате, и на мешочке можно что-то напечатать, а научный сувенир удачно выделит организацию или проект среди прочих. Головоломку несложно изготовить самому и позабавить друзей. Следует лишь учесть, что в зависимости от толщины материала, используемого для изготовления квадрата, мешочек надо сделать с припуском на 1—2 мм относительно «математических» размеров. Нарезаем квадратики и шьём мешочки!
Другие модели раздела «Головоломки»
