Два самых известных определения эллипса — через натянутую ниточку с концами в фокусах и как сечение конуса. Как они связаны? Откуда у сечения конуса берутся эти выделенные точки — фокусы? Почему у эллипса и гиперболы по два фокуса, а у параболы — один? В геометрическом определении параболы участвует директриса. А есть ли директриса у эллипса и, если да, то что это такое? Свести факты о кониках в единую картину позволяют сферы (шары) Данделена.
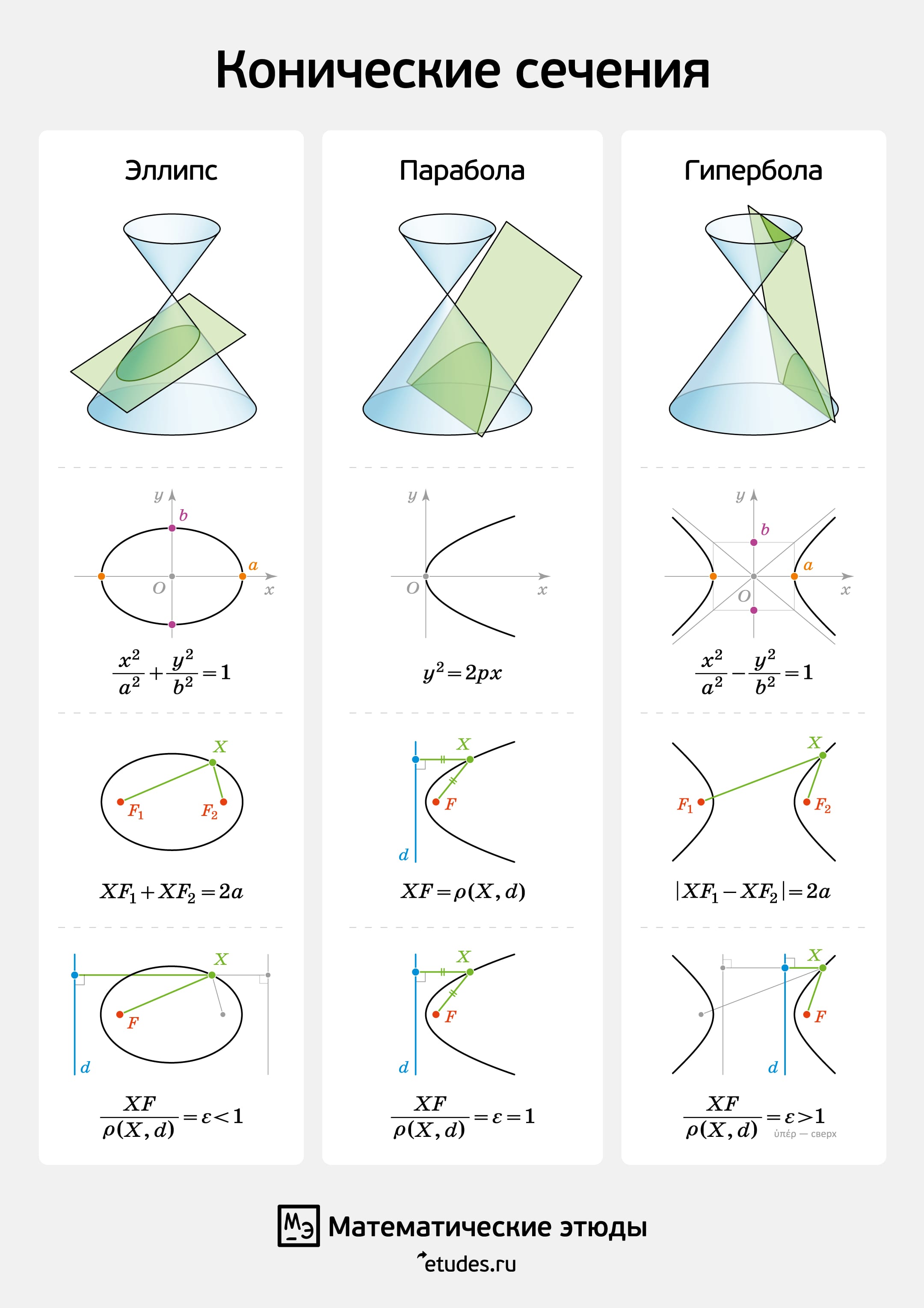
Каждое коническое сечение — эллипс, парабола, гипербола — имеет несколько (эквивалентных) определений: как невырожденное сечение конуса; алгебраическое — задание уравнением; геометрическое — через фокусы; через эксцентриситет.
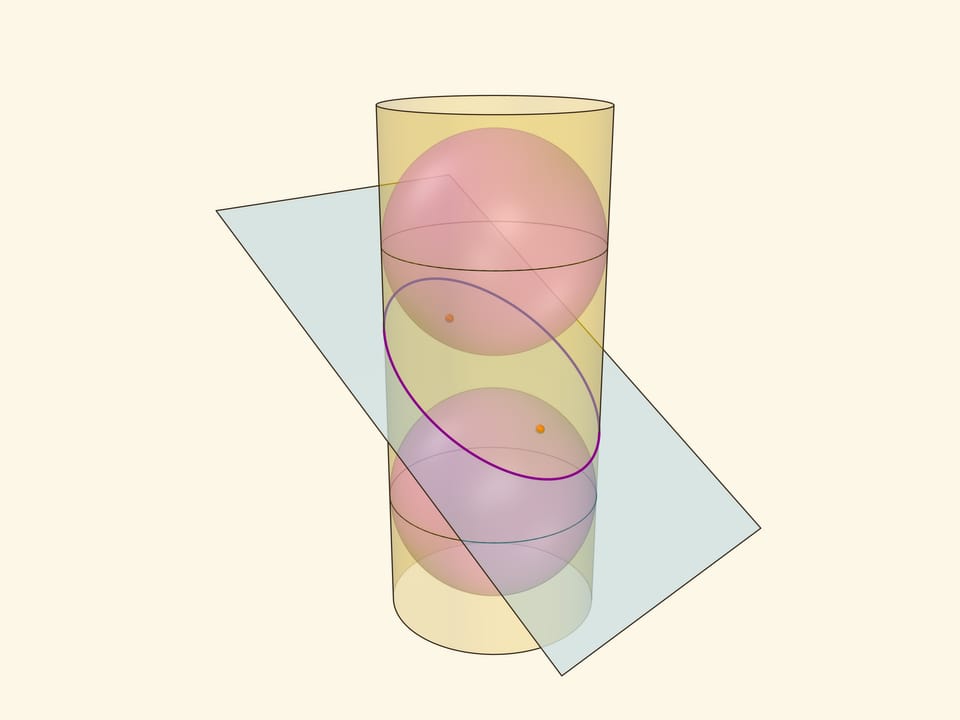
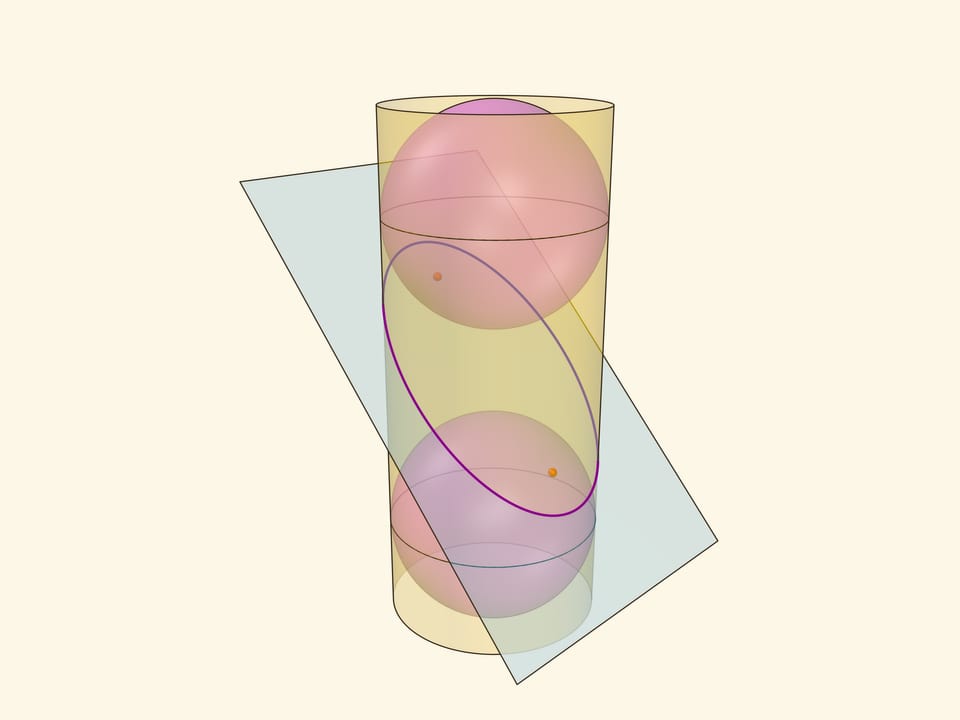
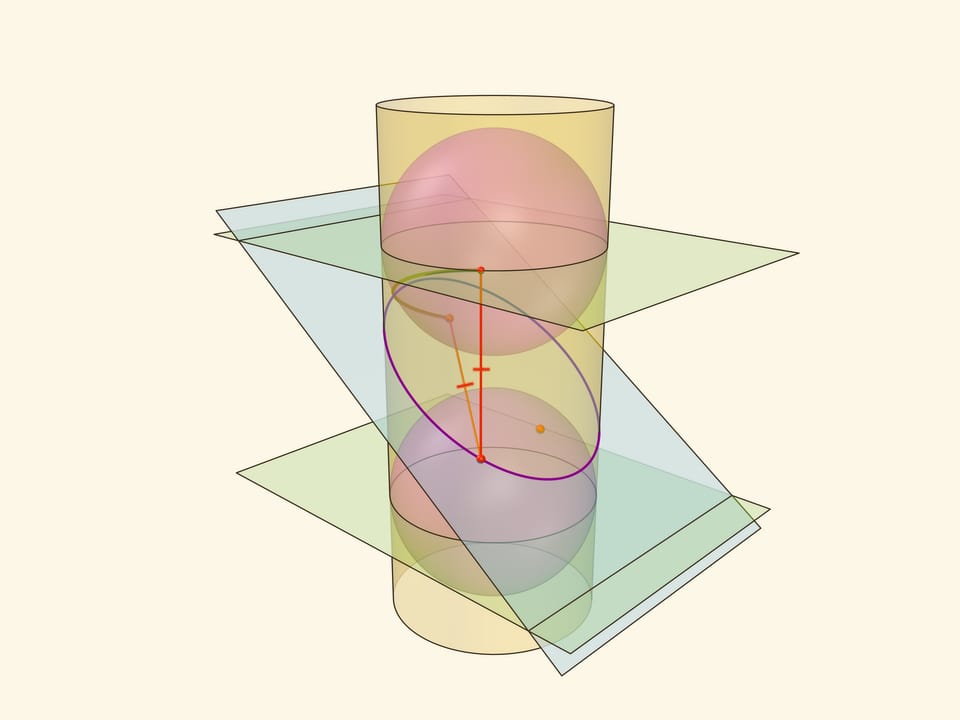
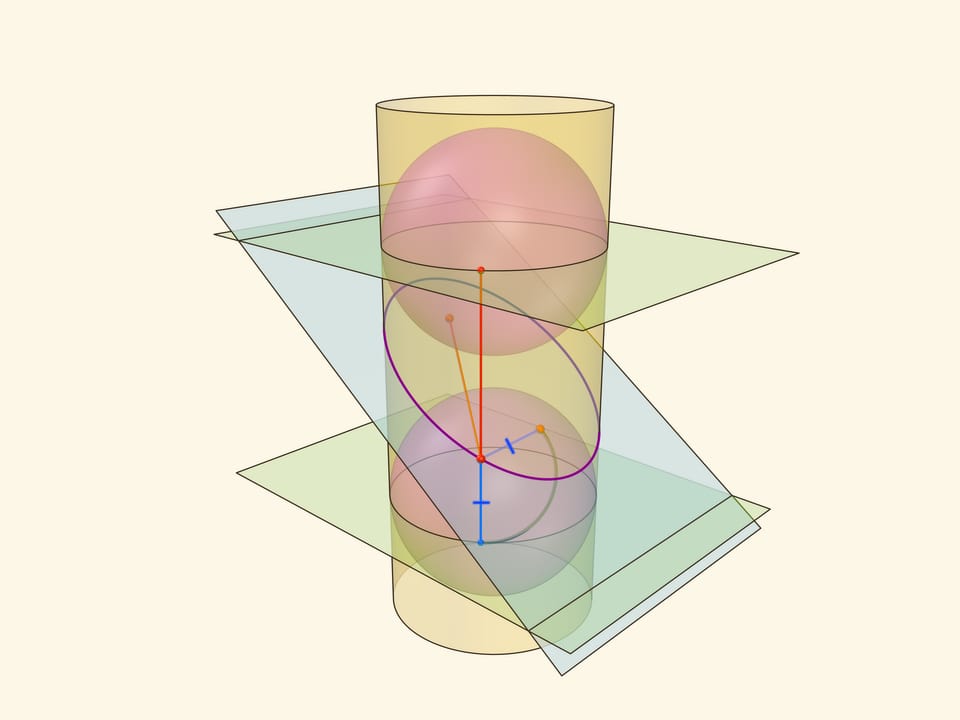
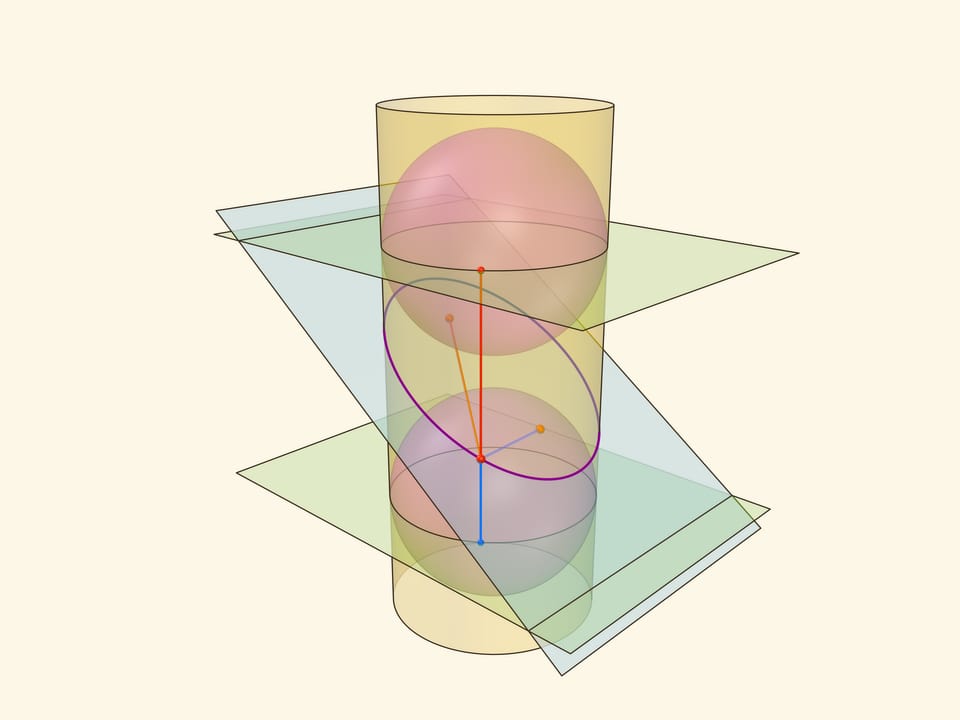
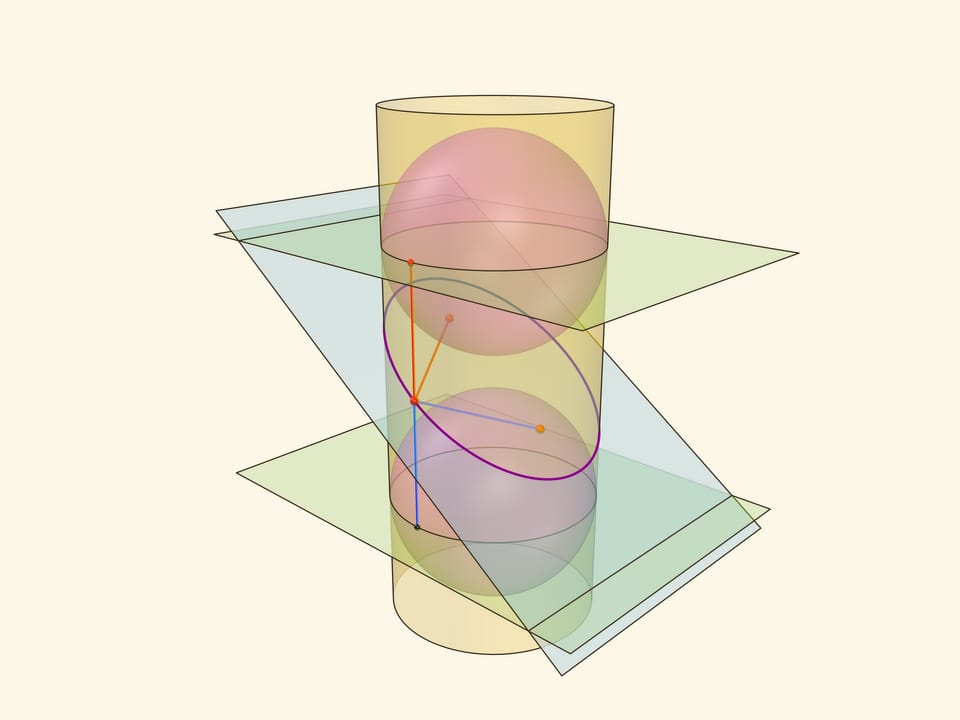
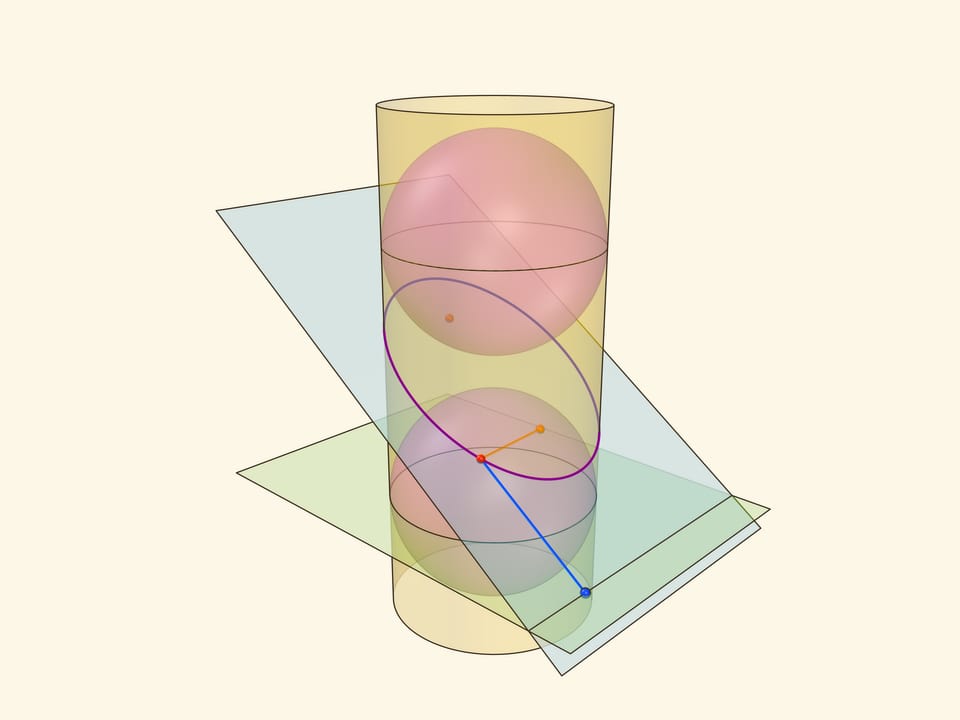
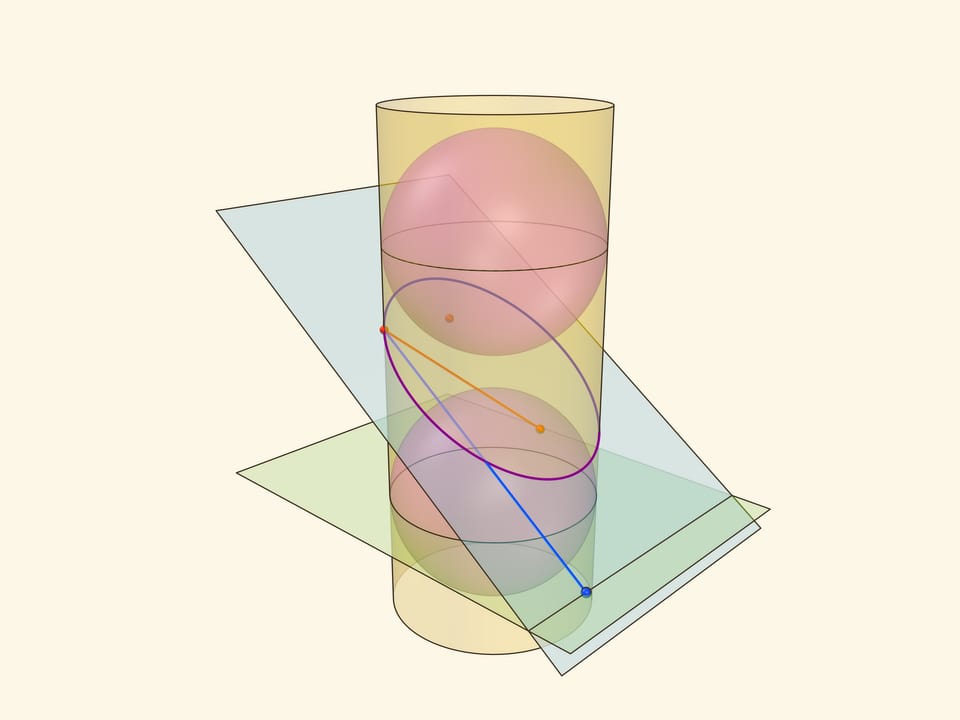
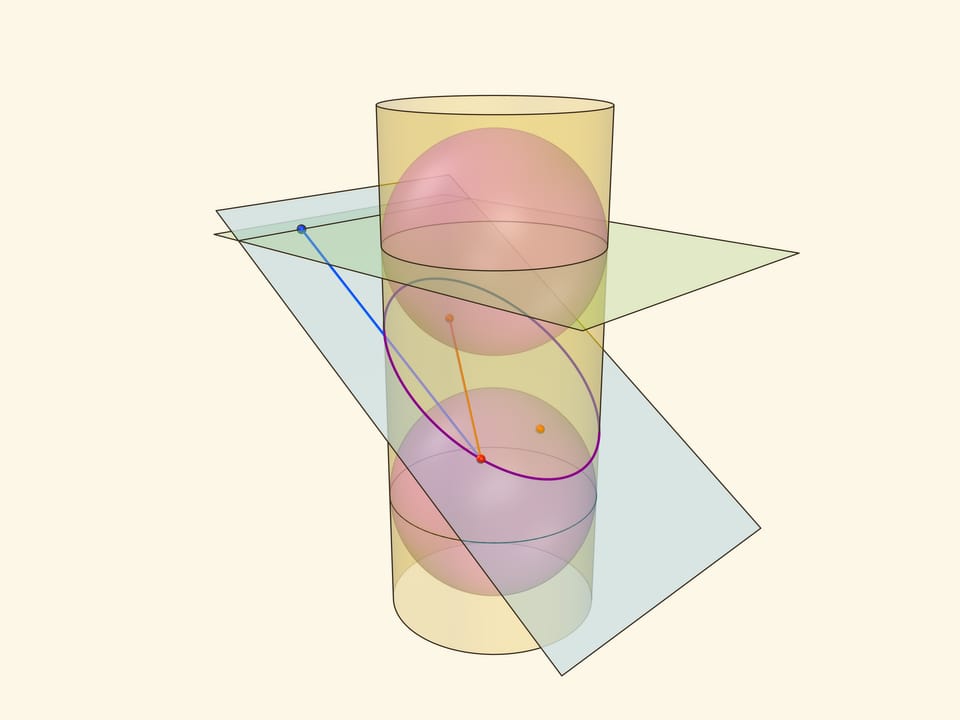
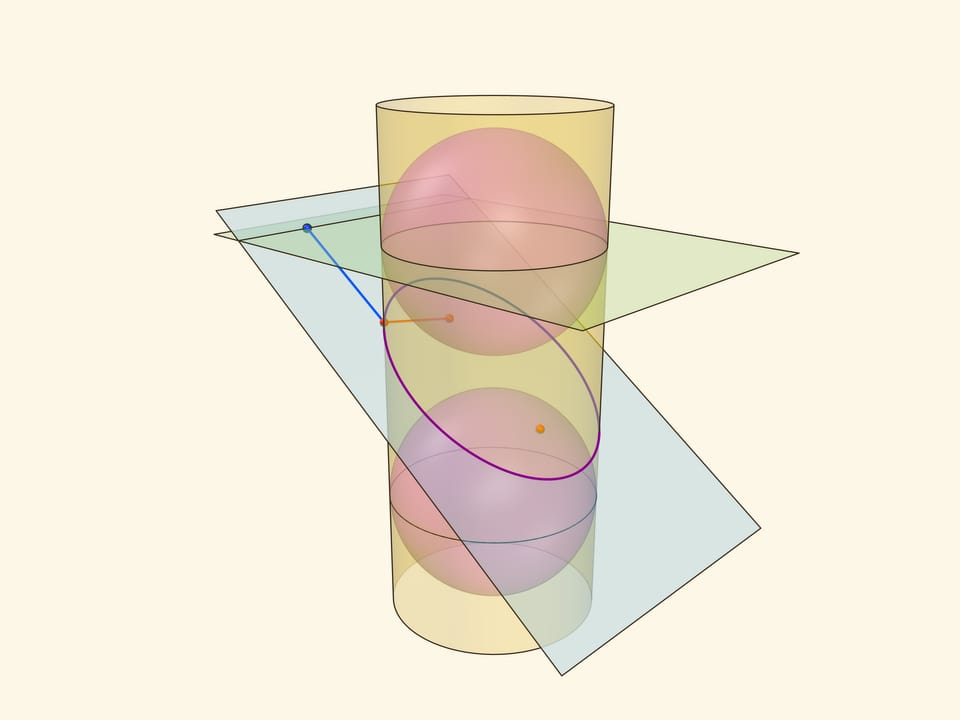
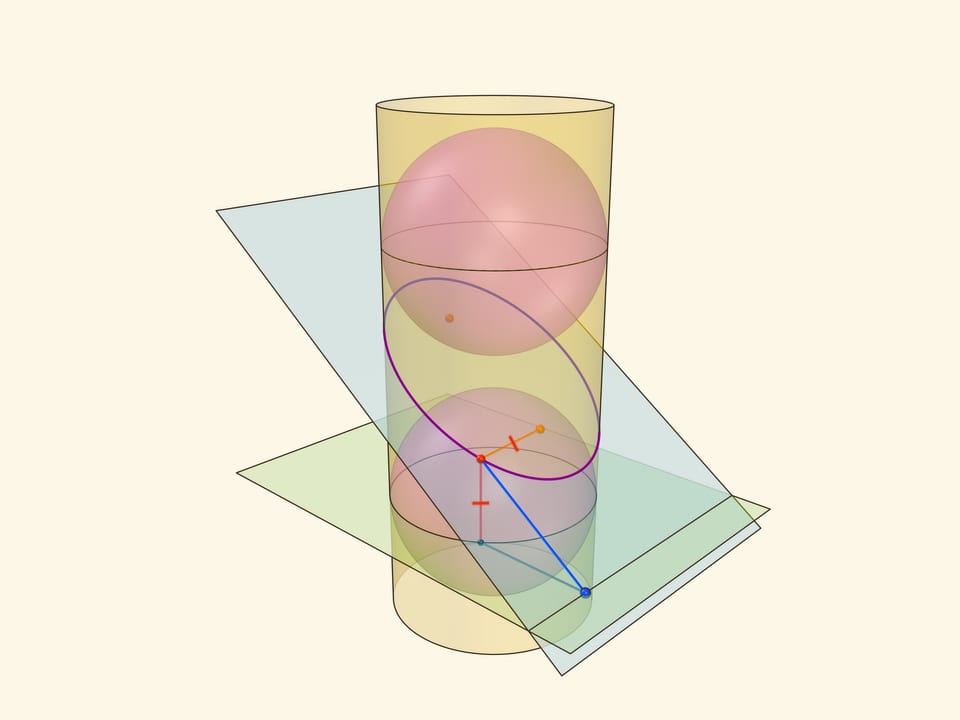
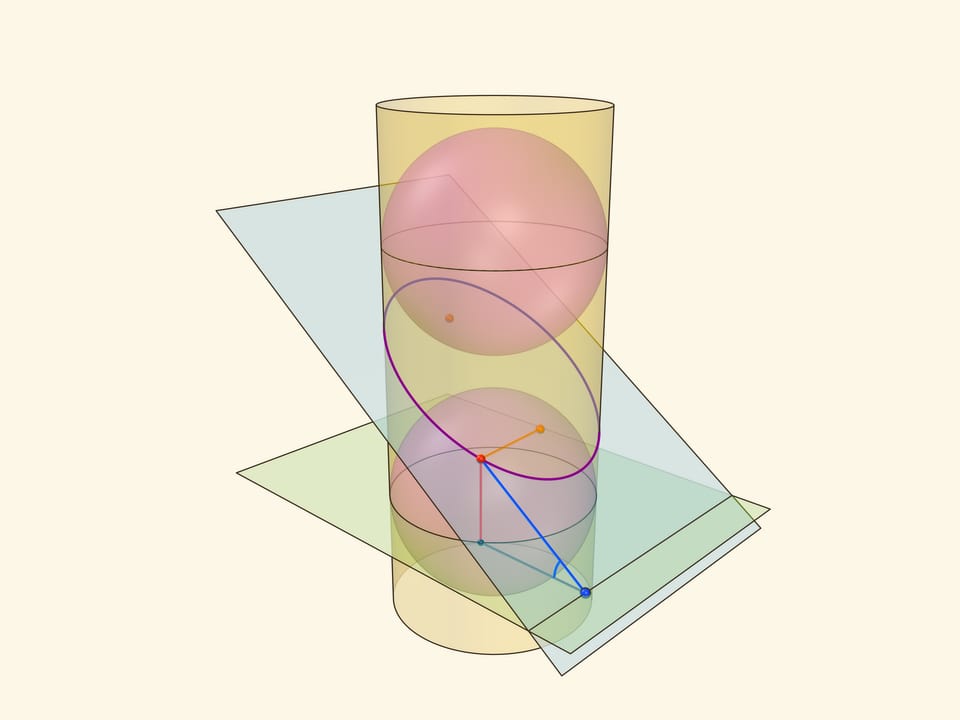
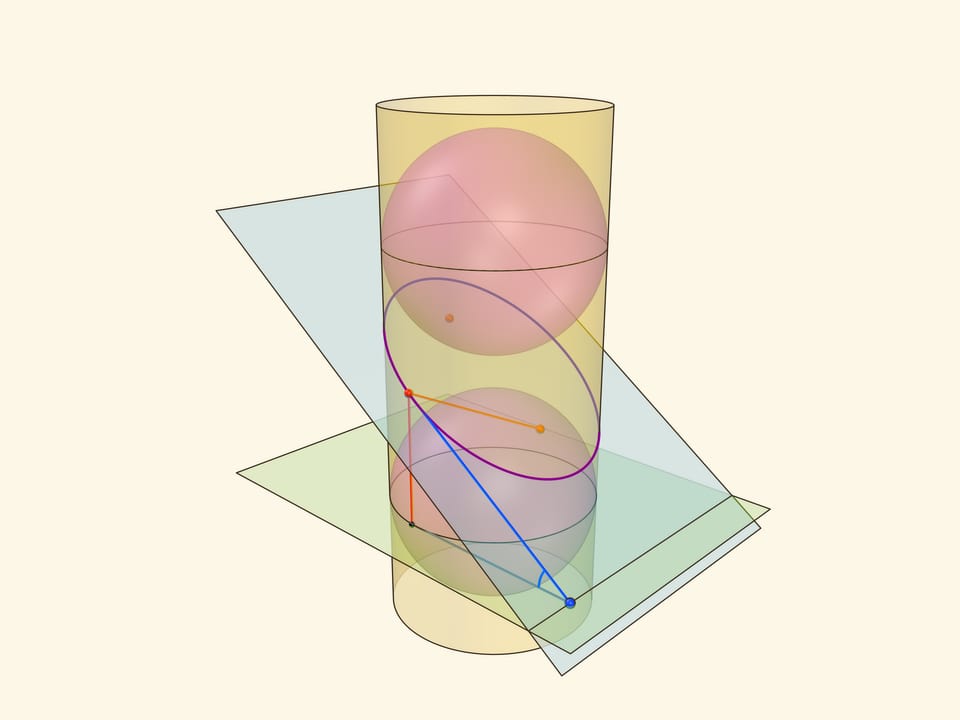
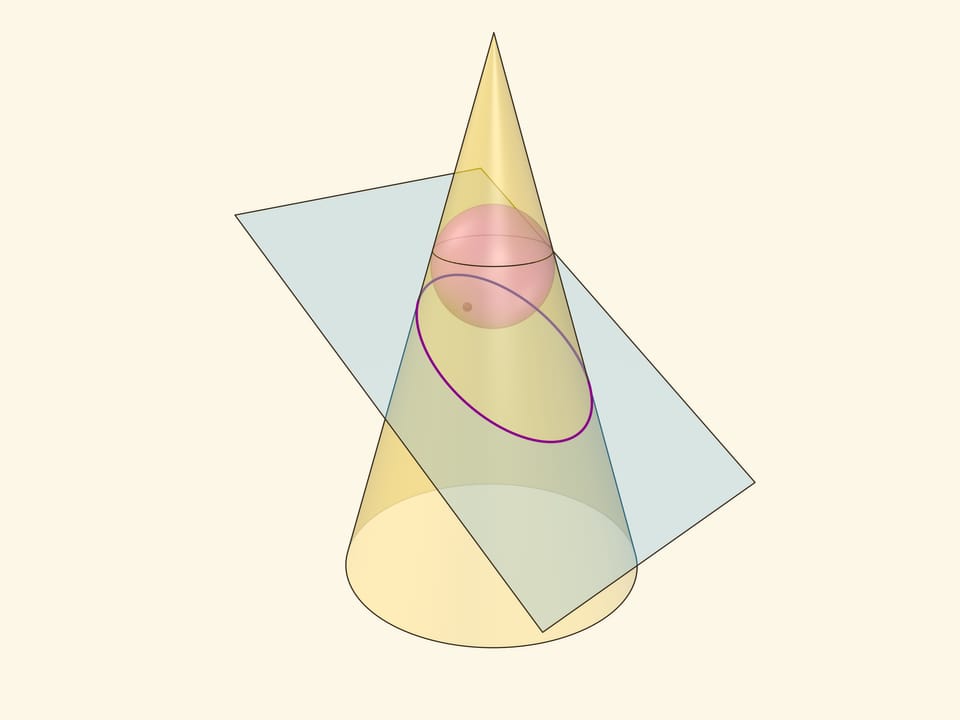
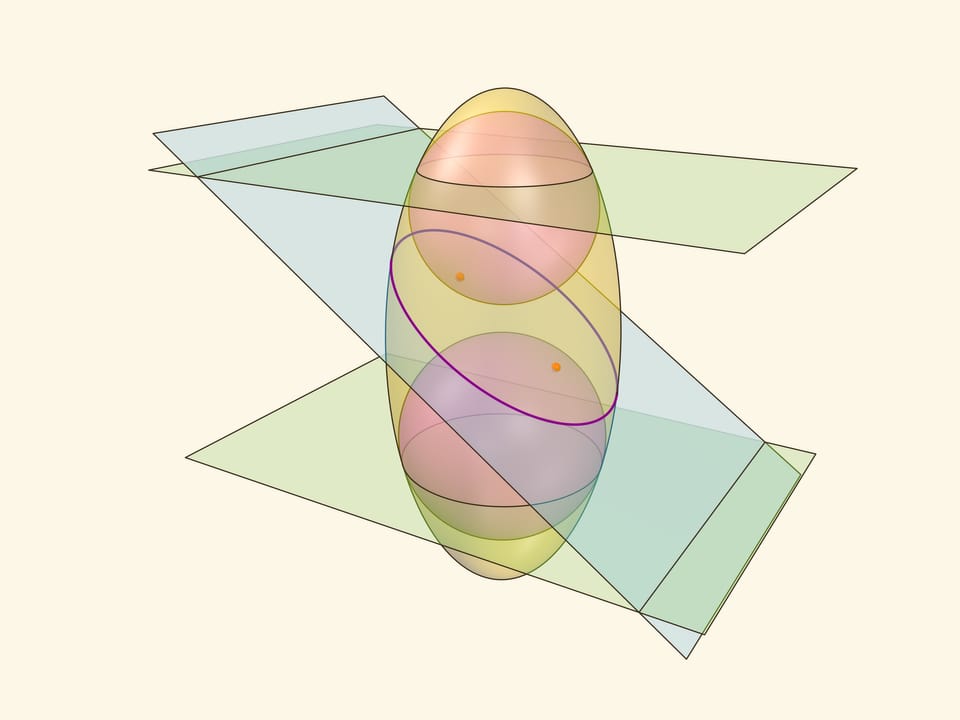
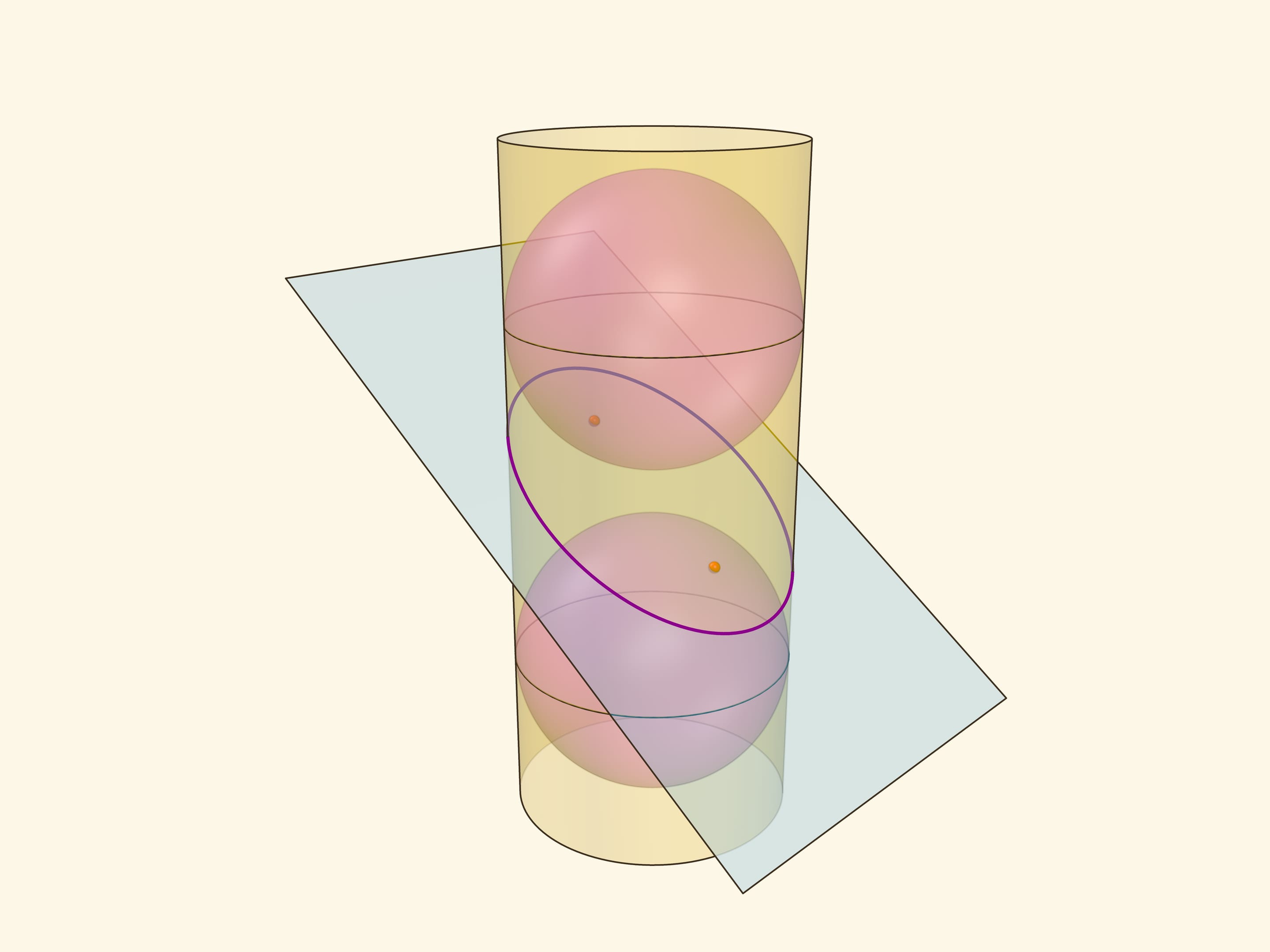
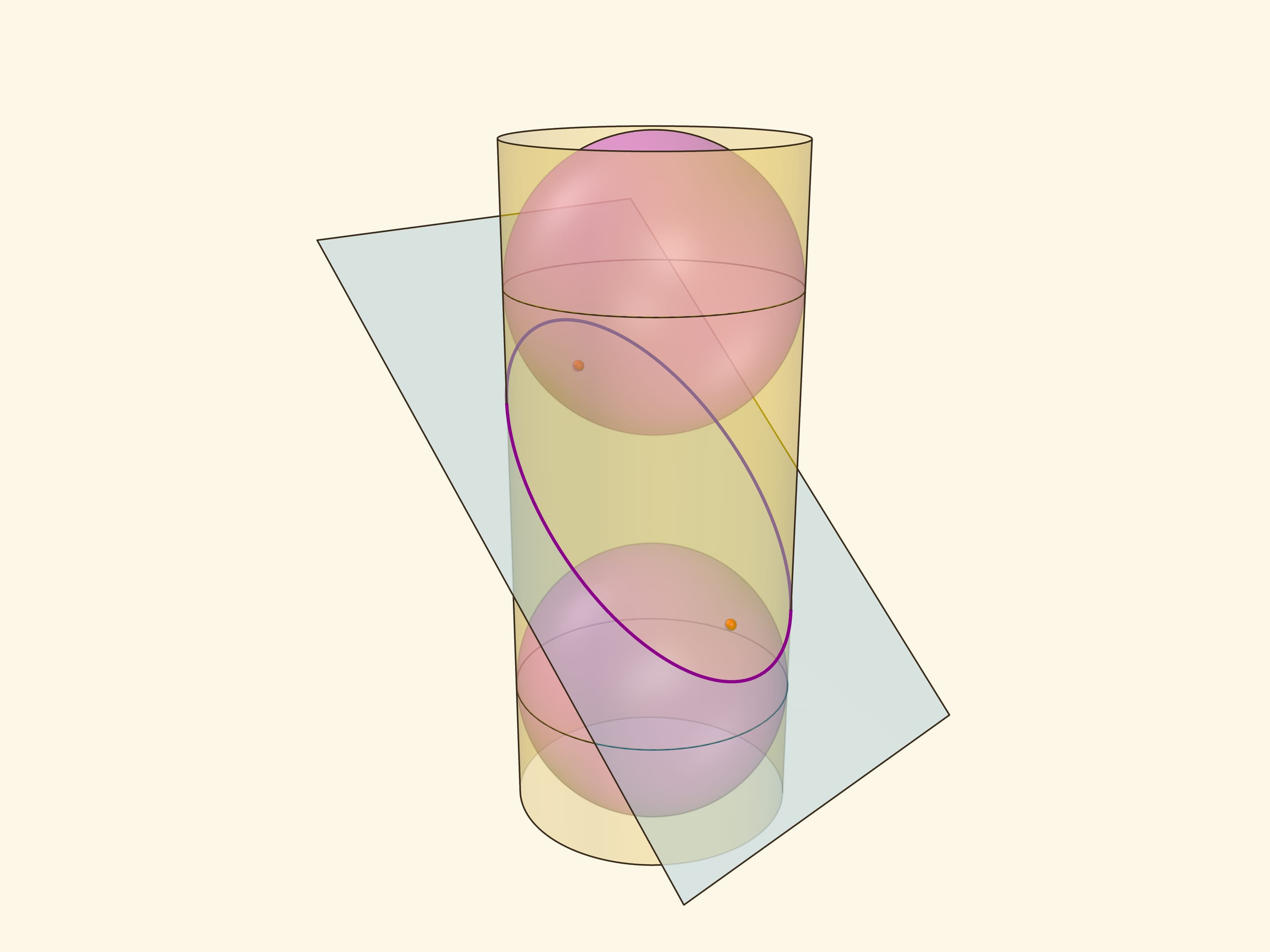
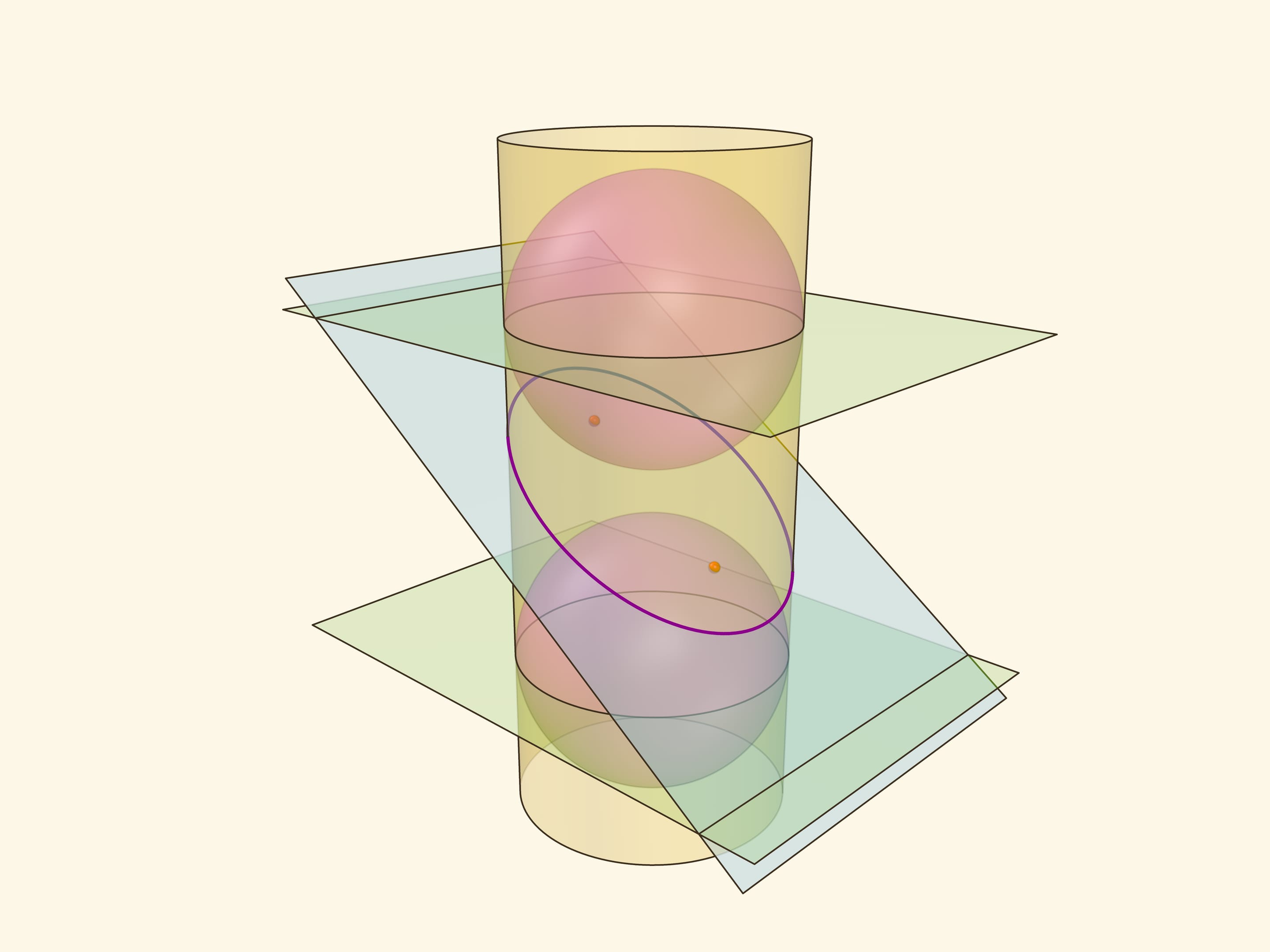
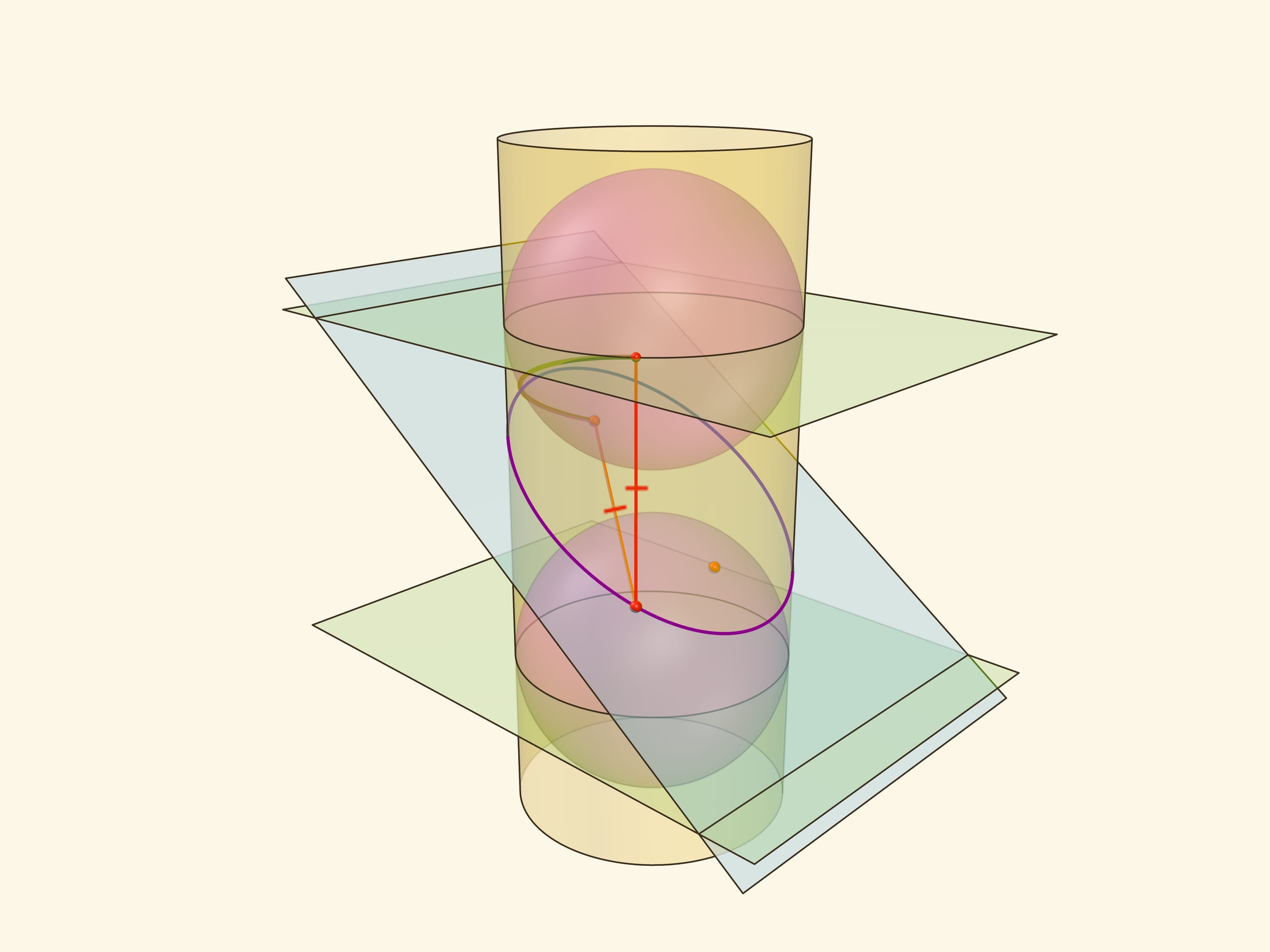
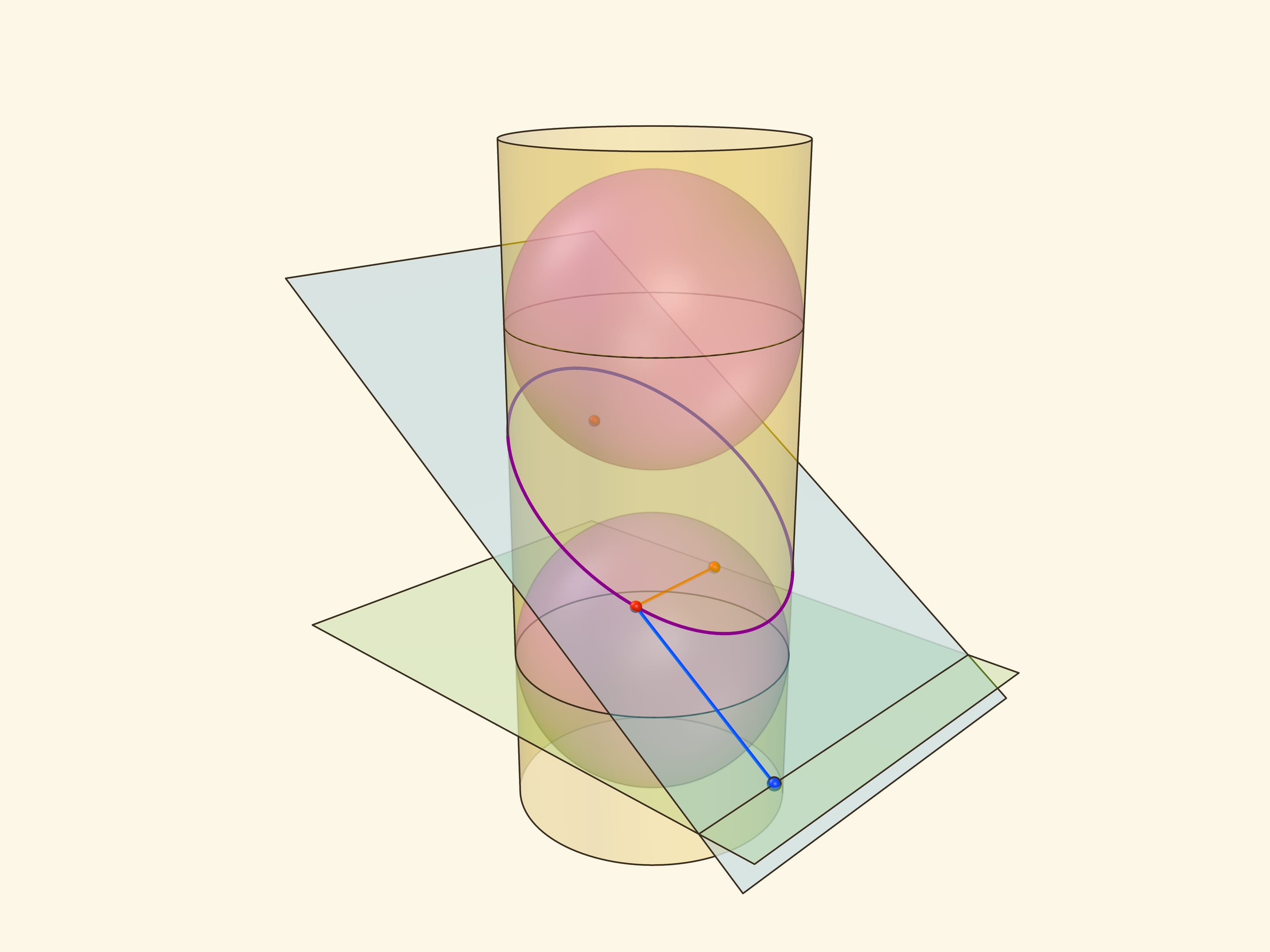
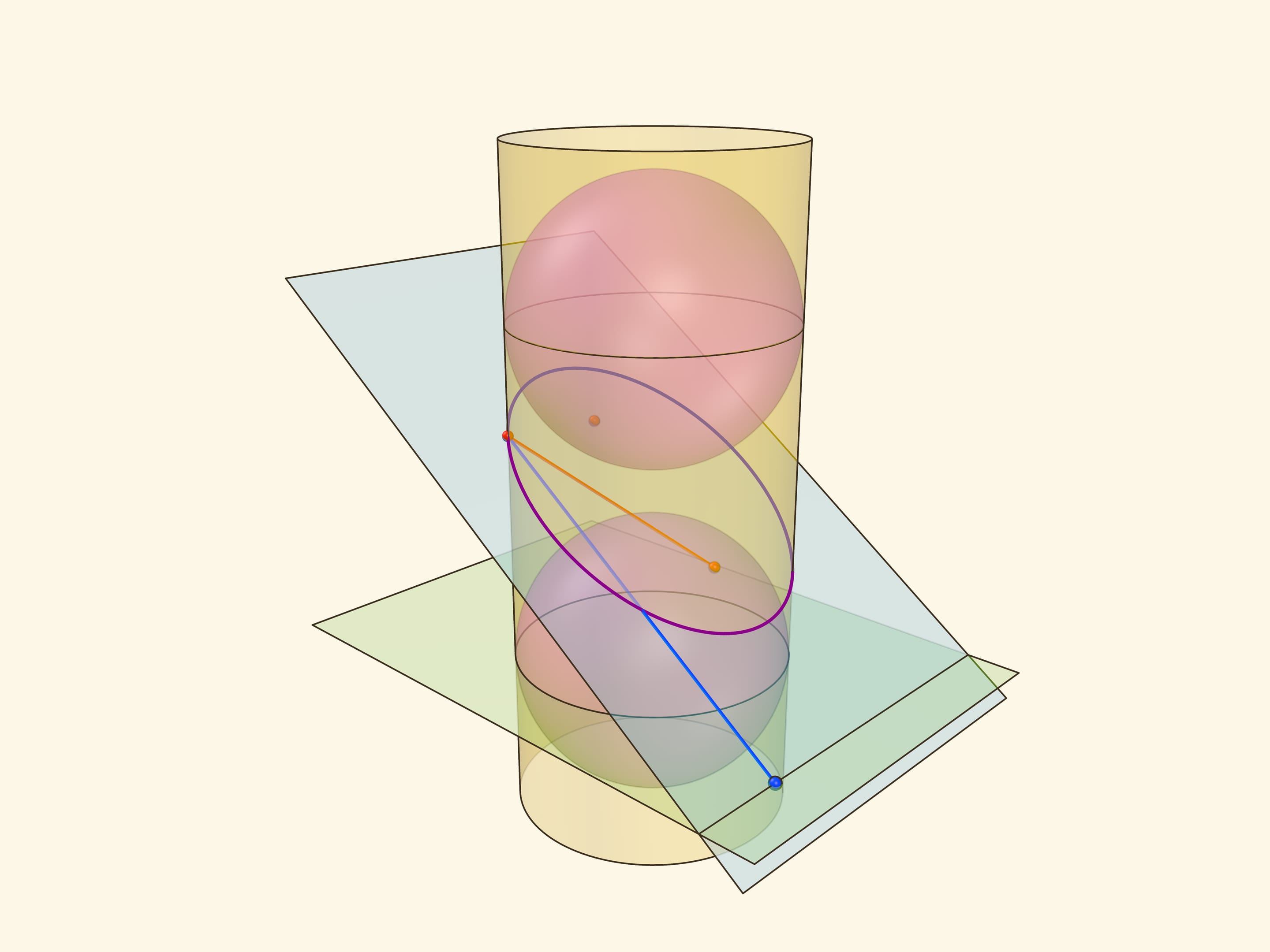
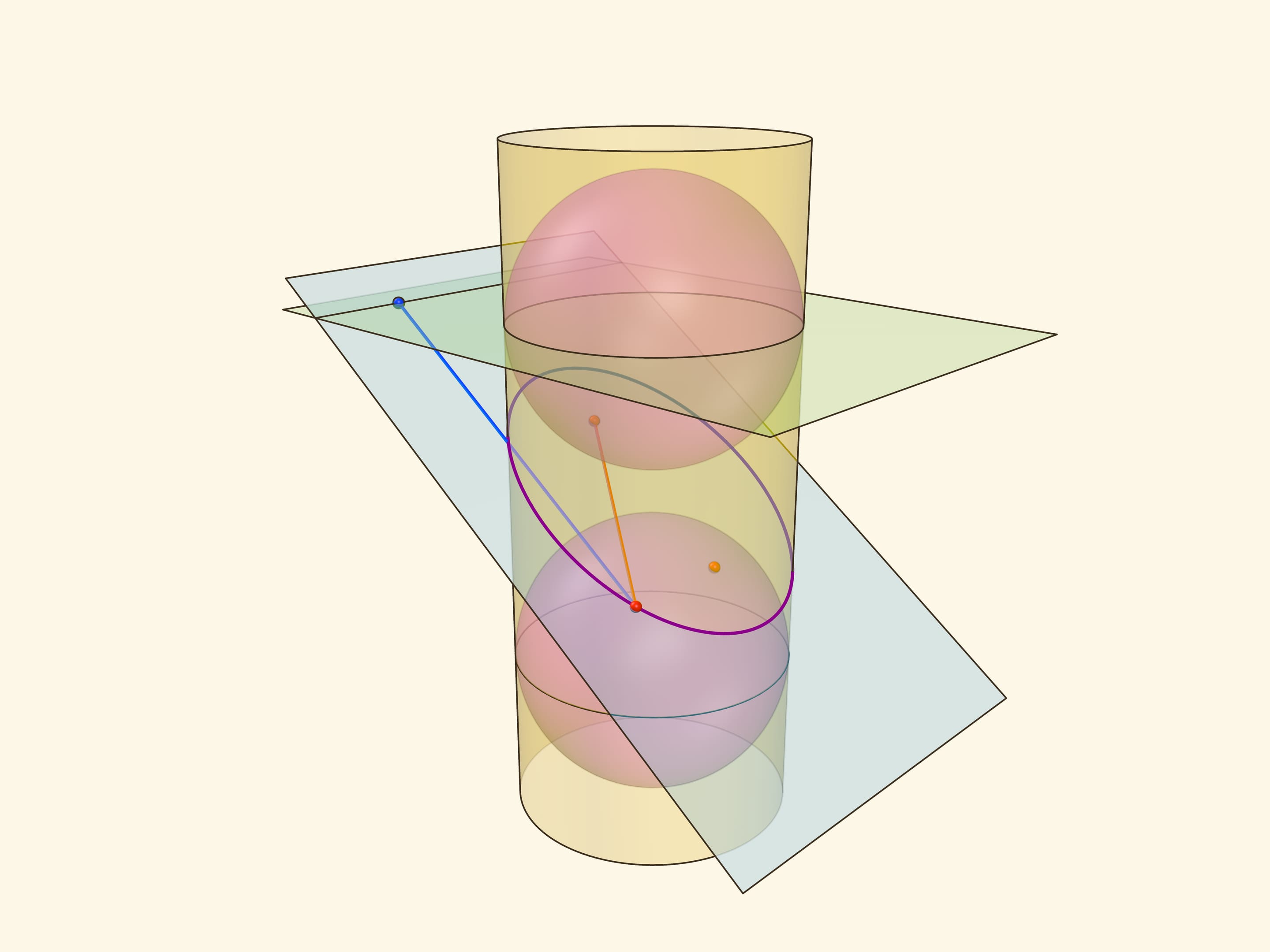
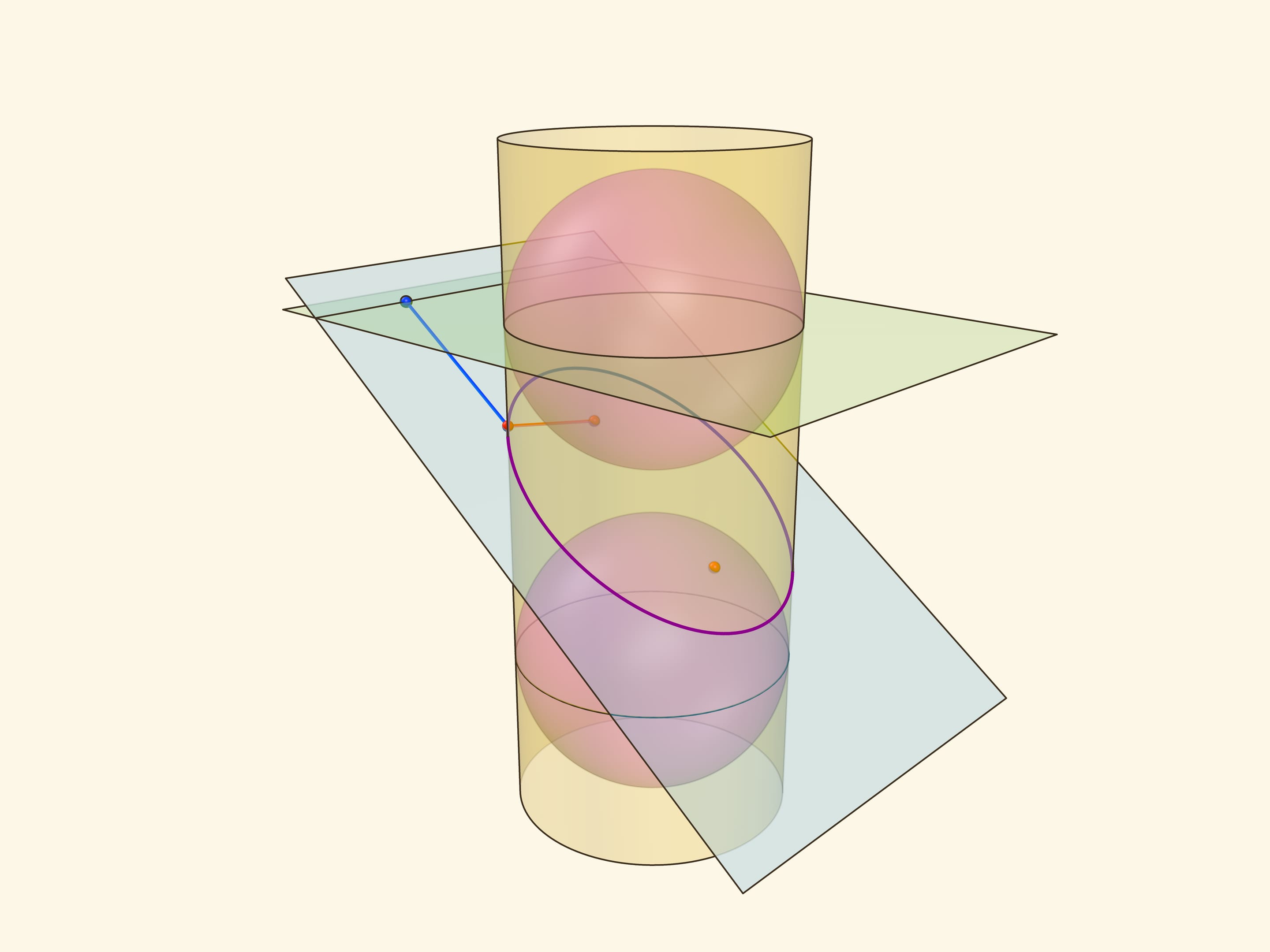
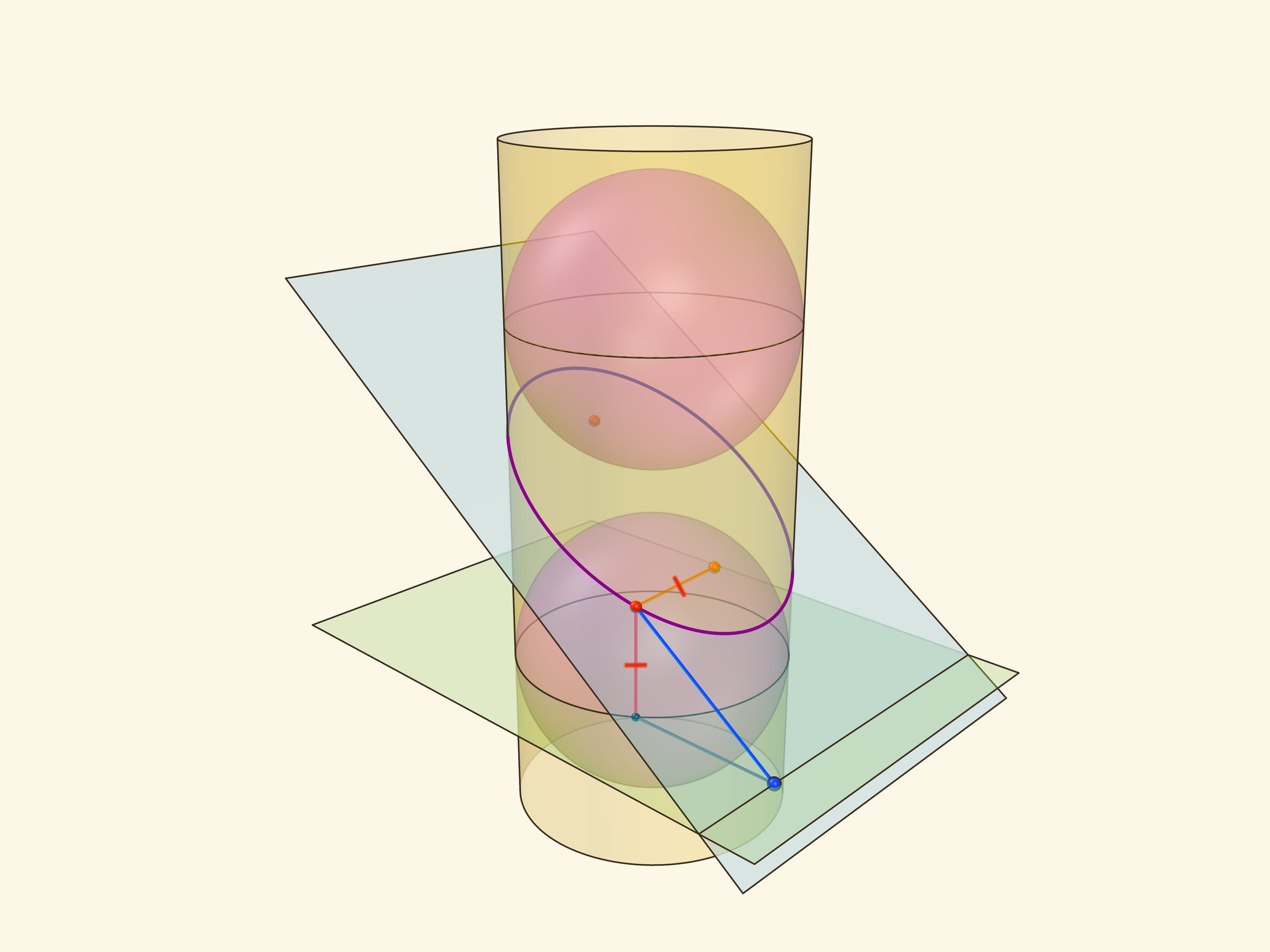
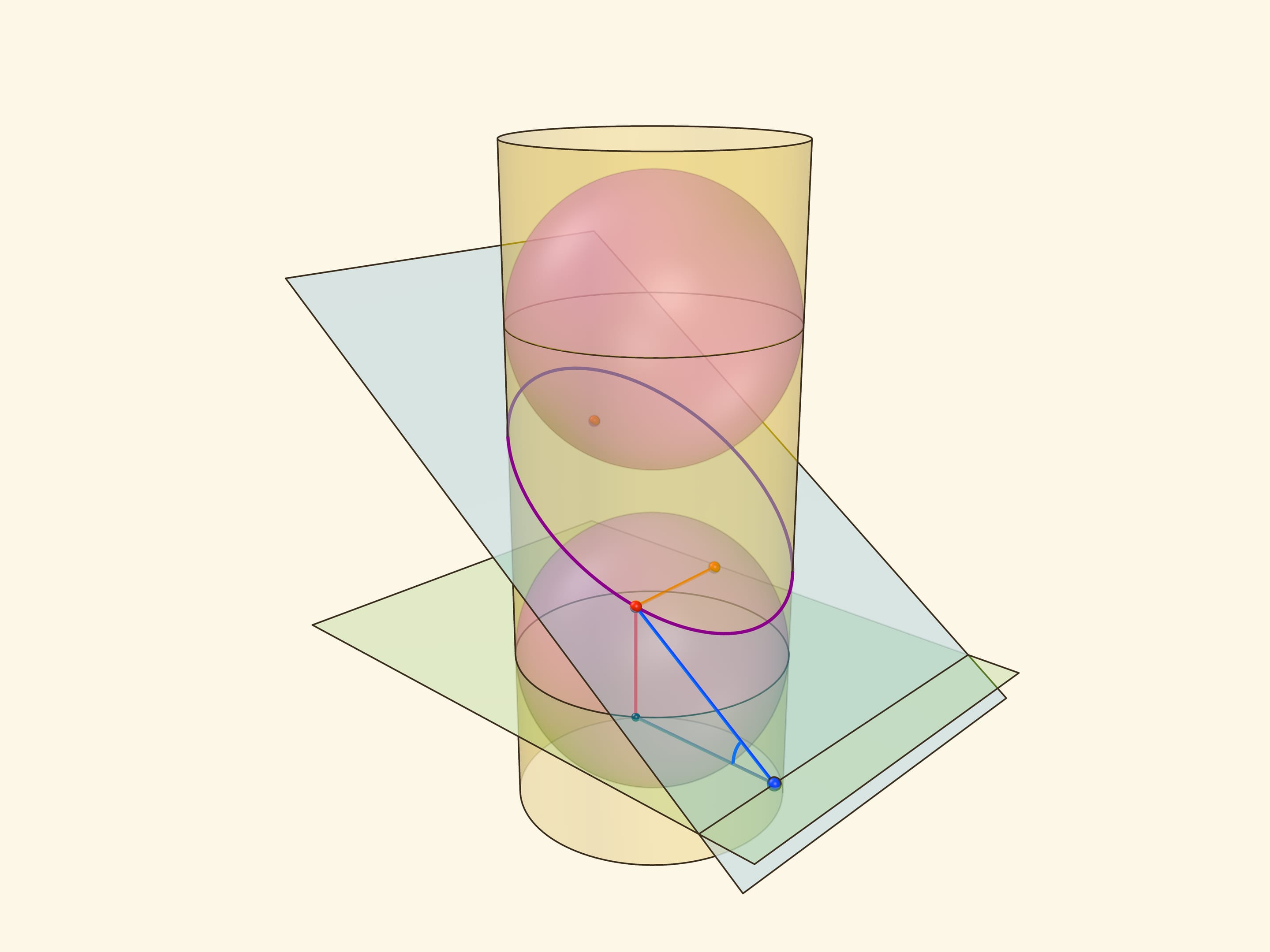
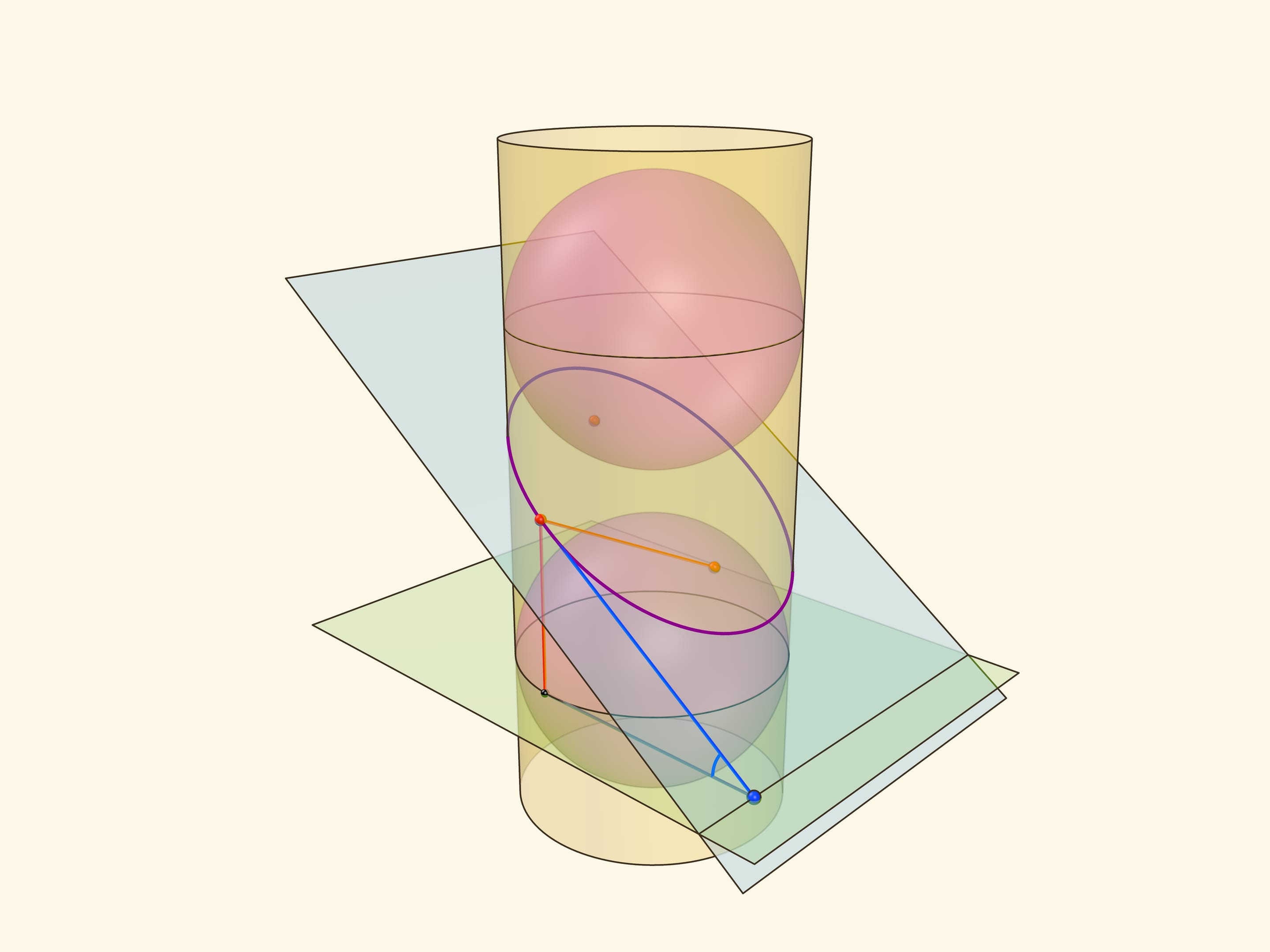
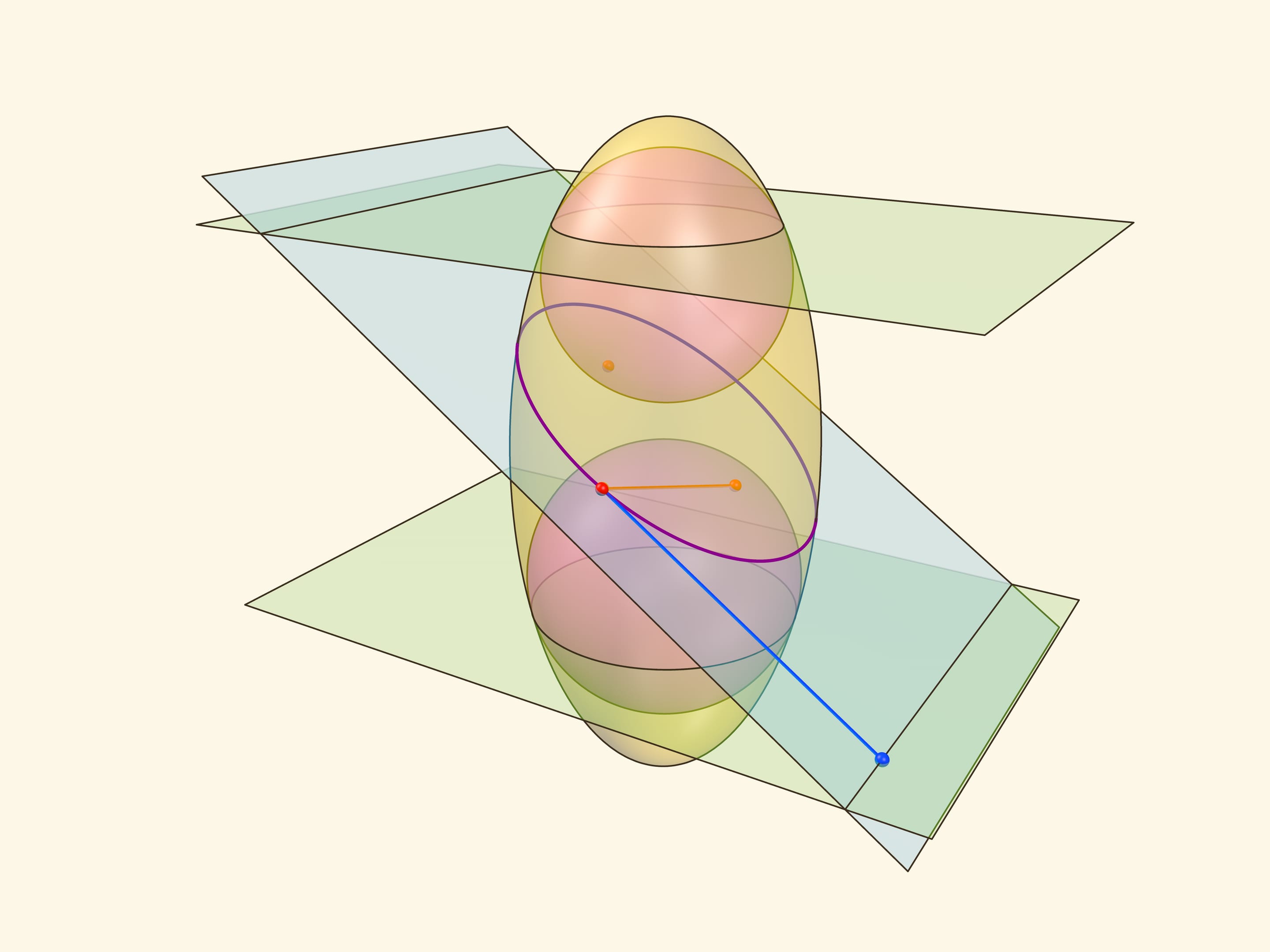
Эллипс можно получить не только как сечение конуса, но и как сечение (прямого кругового) цилиндра плоскостью, непараллельной его оси. Впишем в цилиндр два шара и придвинем их к секущей плоскости так, чтобы они её коснулись с разных сторон. Это и есть сферы Данделена, а точки касания с секущей плоскостью — фокусы эллипса.
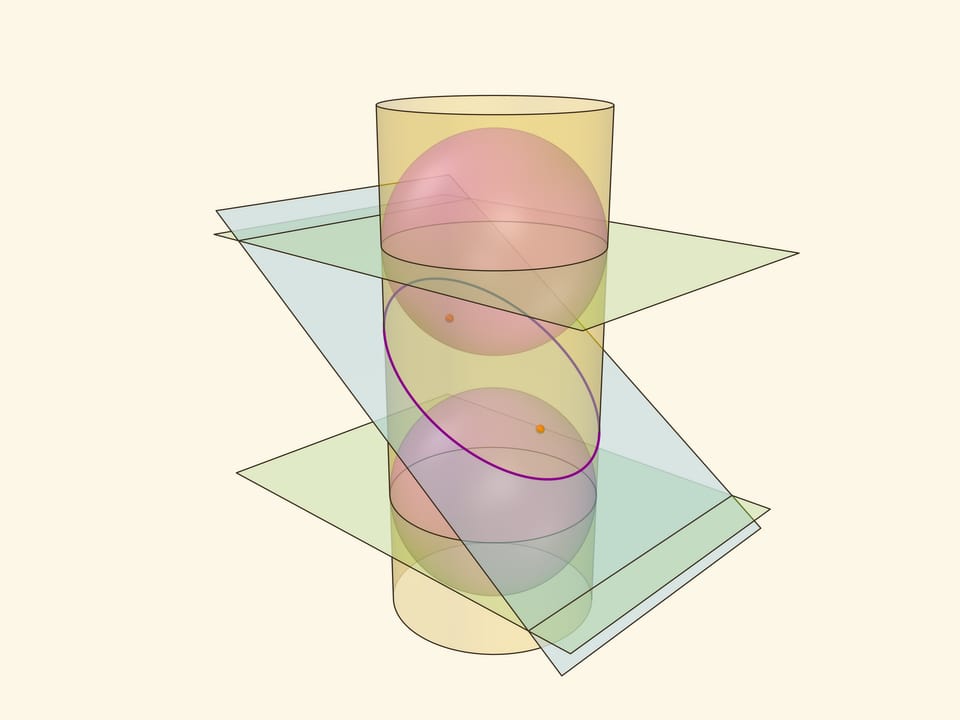
Через окружности касания сфер Данделена с цилиндром проведём две параллельные «горизонтальные» плоскости до пересечения с секущей плоскостью. Линии пересечения — директрисы эллипса.
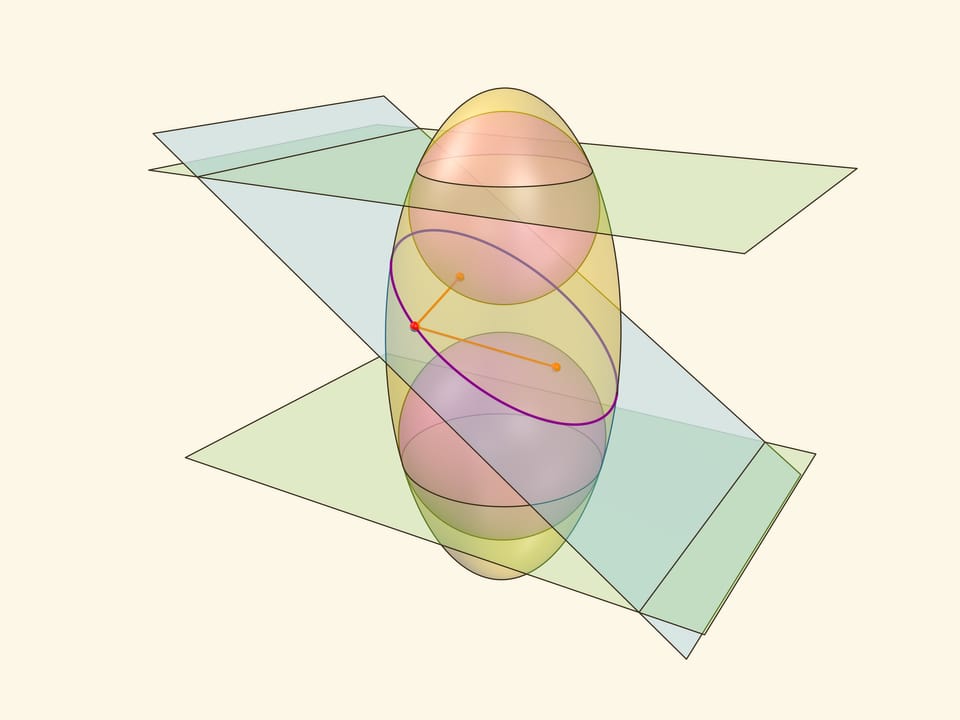
Докажем, что из определения эллипса как сечения цилиндра следует геометрическое определение эллипса. Воспользуемся тем, что касательные к сфере, проведённые из одной точки, равны.
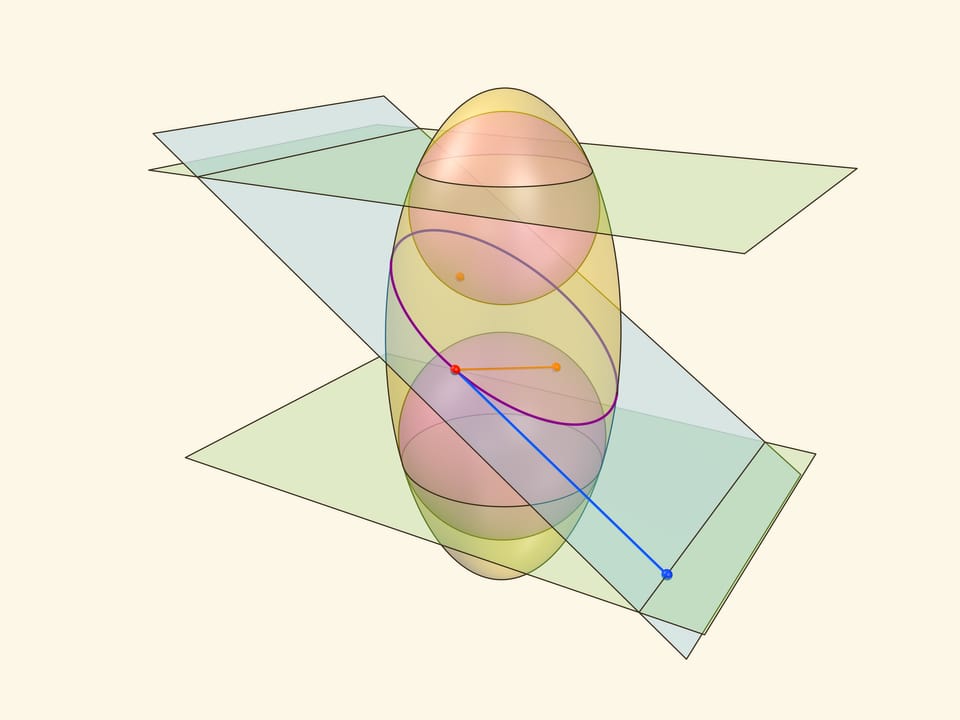
Отрезок от точки эллипса до фокуса равен отрезку образующей цилиндра от точки эллипса до окружности касания цилиндра и сферы Данделена, давшей данный фокус. Со вторым фокусом так же. В итоге сумма расстояний от точки до фокусов равна длине отрезка образующей цилиндра между параллельными плоскостями. Но эта длина не зависит от рассматриваемой точки эллипса, она всегда постоянна.
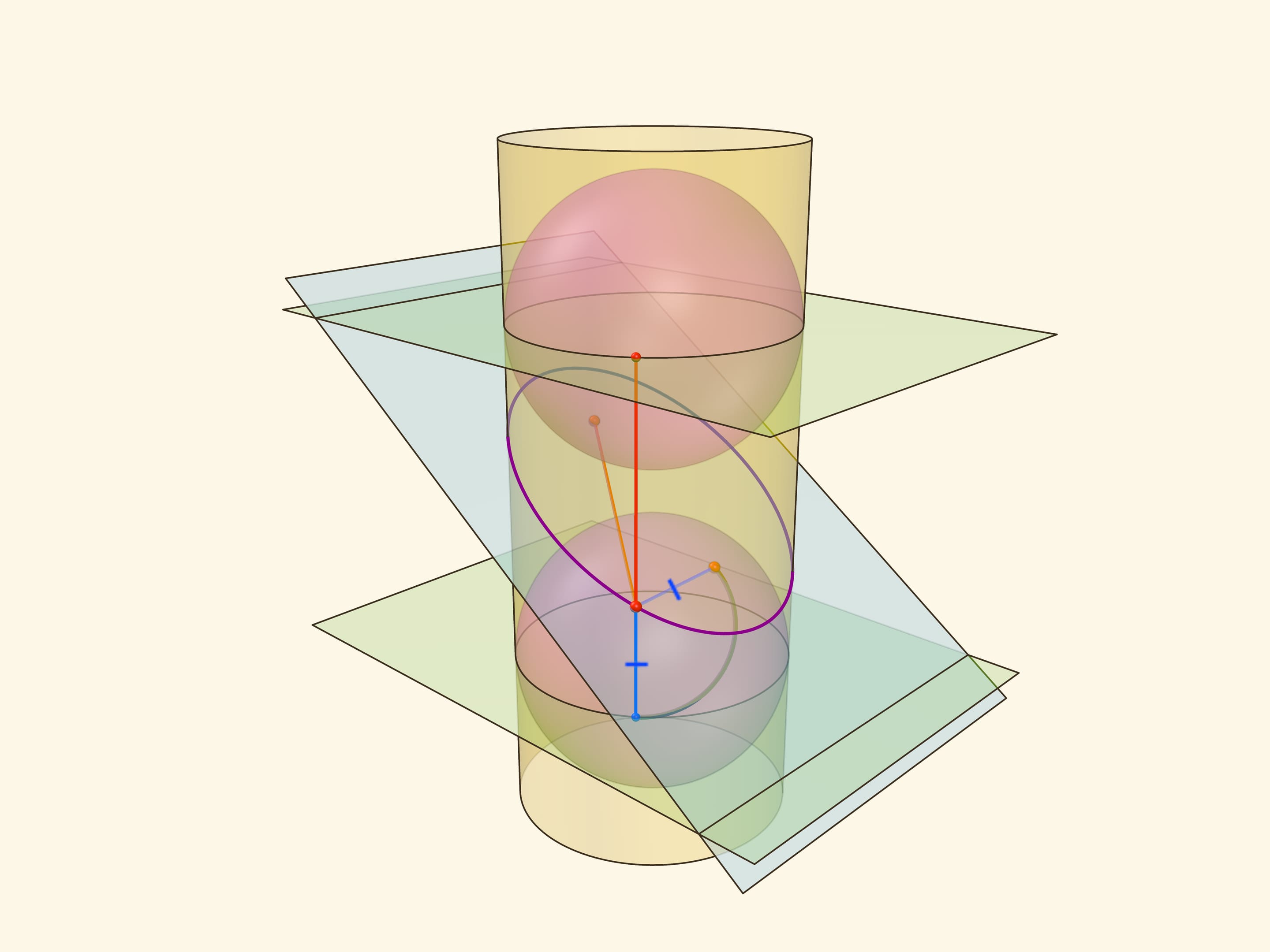
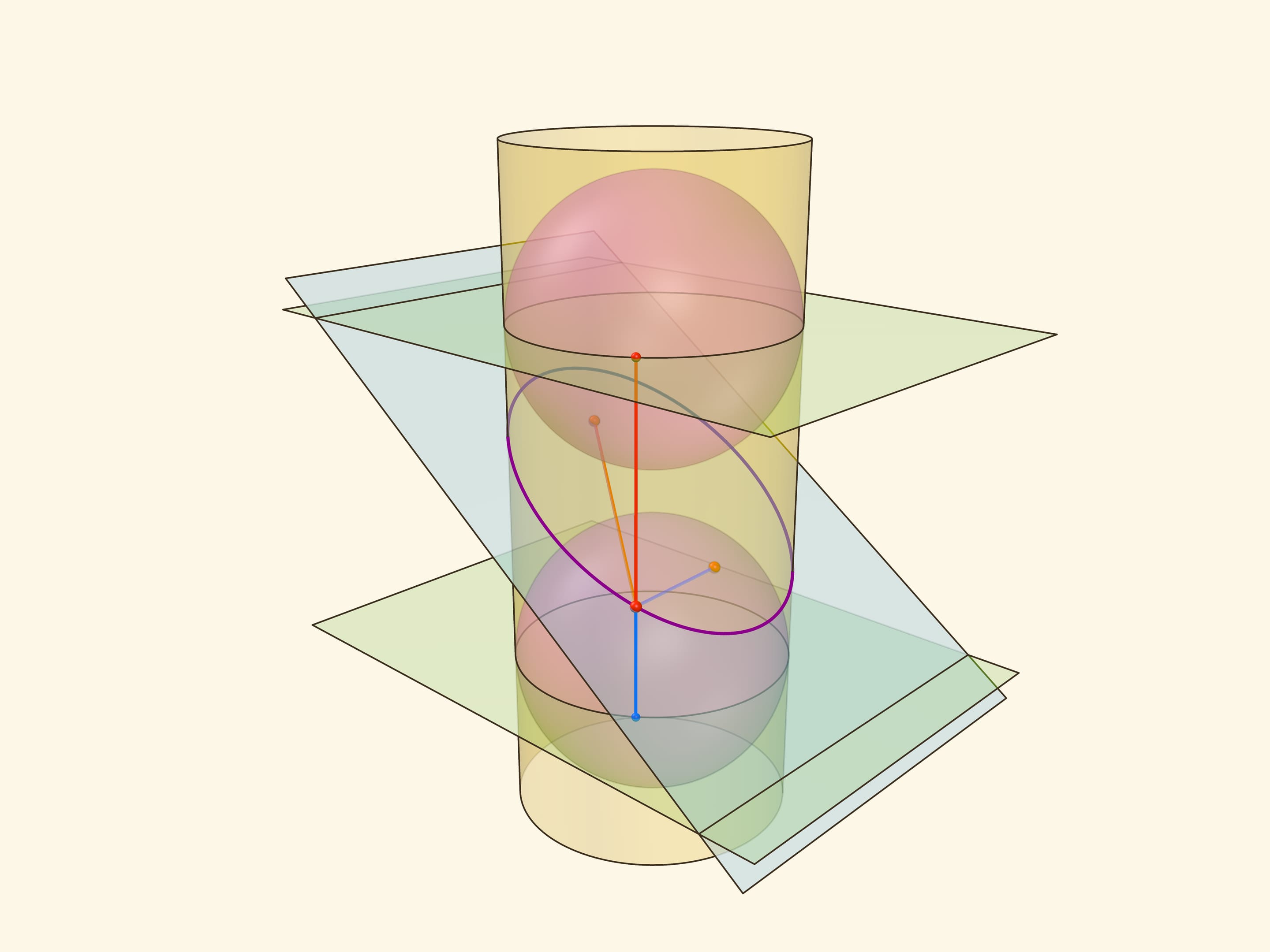
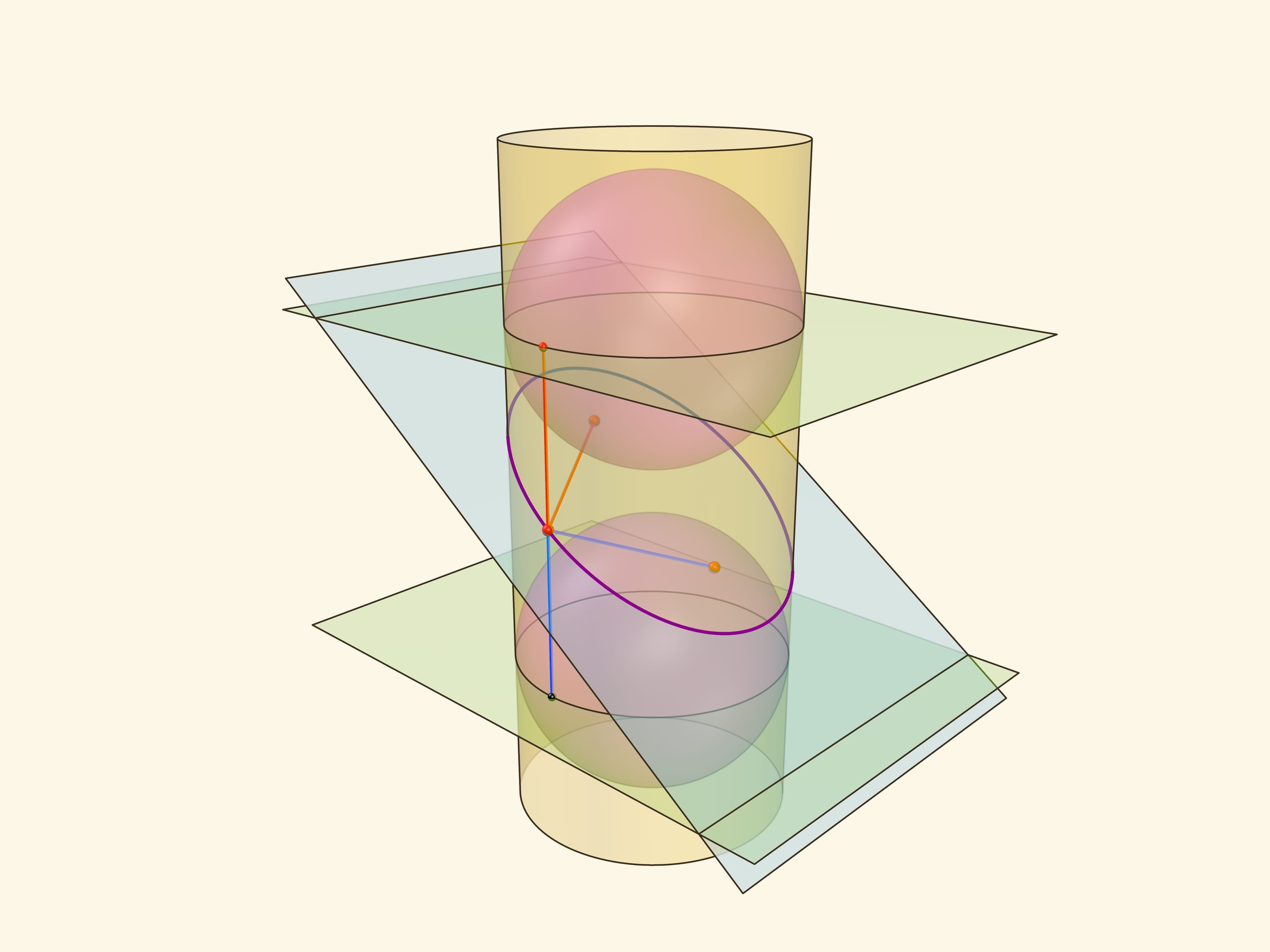
Покажем, что прямые, являющиеся пересечением горизонтальных плоскостей с секущей, являются директрисами: отношение расстояния от точки до фокуса к расстоянию от точки до прямой всегда постоянно. Это отношение называют эксцентриситетом и обозначают греческой буквой $\varepsilon$.
Из точки на эллипсе опустим перпендикуляр на горизонтальную плоскость. В возникшем прямоугольном треугольнике расстояние от точки до директрисы есть гипотенуза, а катет равен расстоянию от точки до фокуса (так как оба отрезка касаются сферы). Таким образом, рассматриваемое отношение равно синусу двугранного угла между секущей и горизонтальной плоскостями: и гипотенуза, и катет перпендикулярны линии пересечения плоскостей. И так как эллипс лежит в секущей плоскости, то для любой его точки этот угол, а стало быть, и отношение расстояний, не меняется. Это и есть эксцентриситет эллипса, он всегда меньше 1.
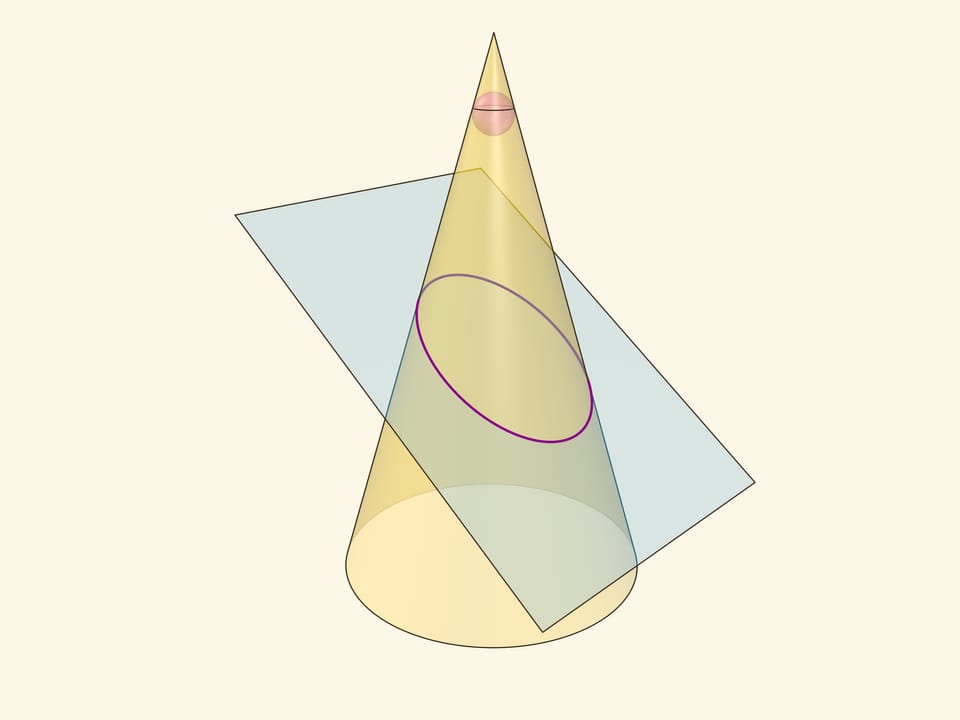
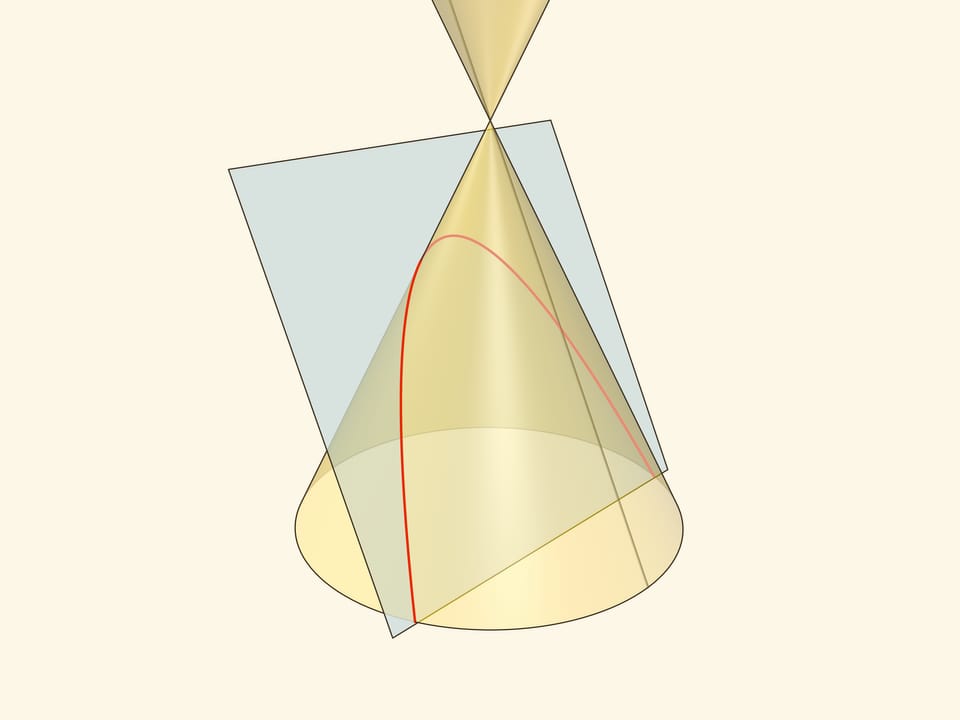
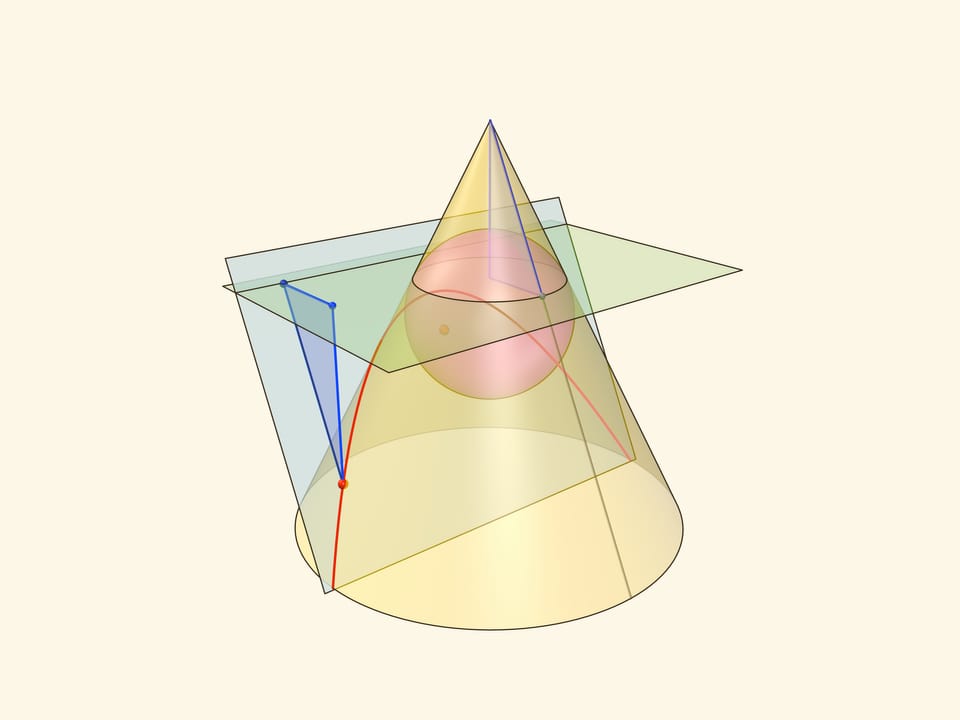
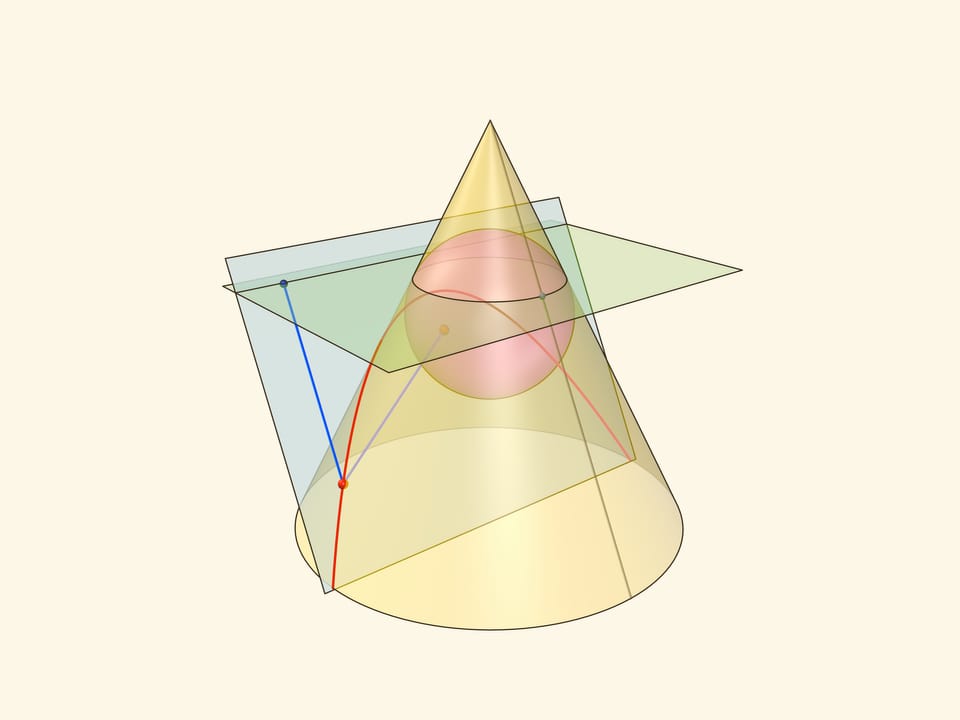
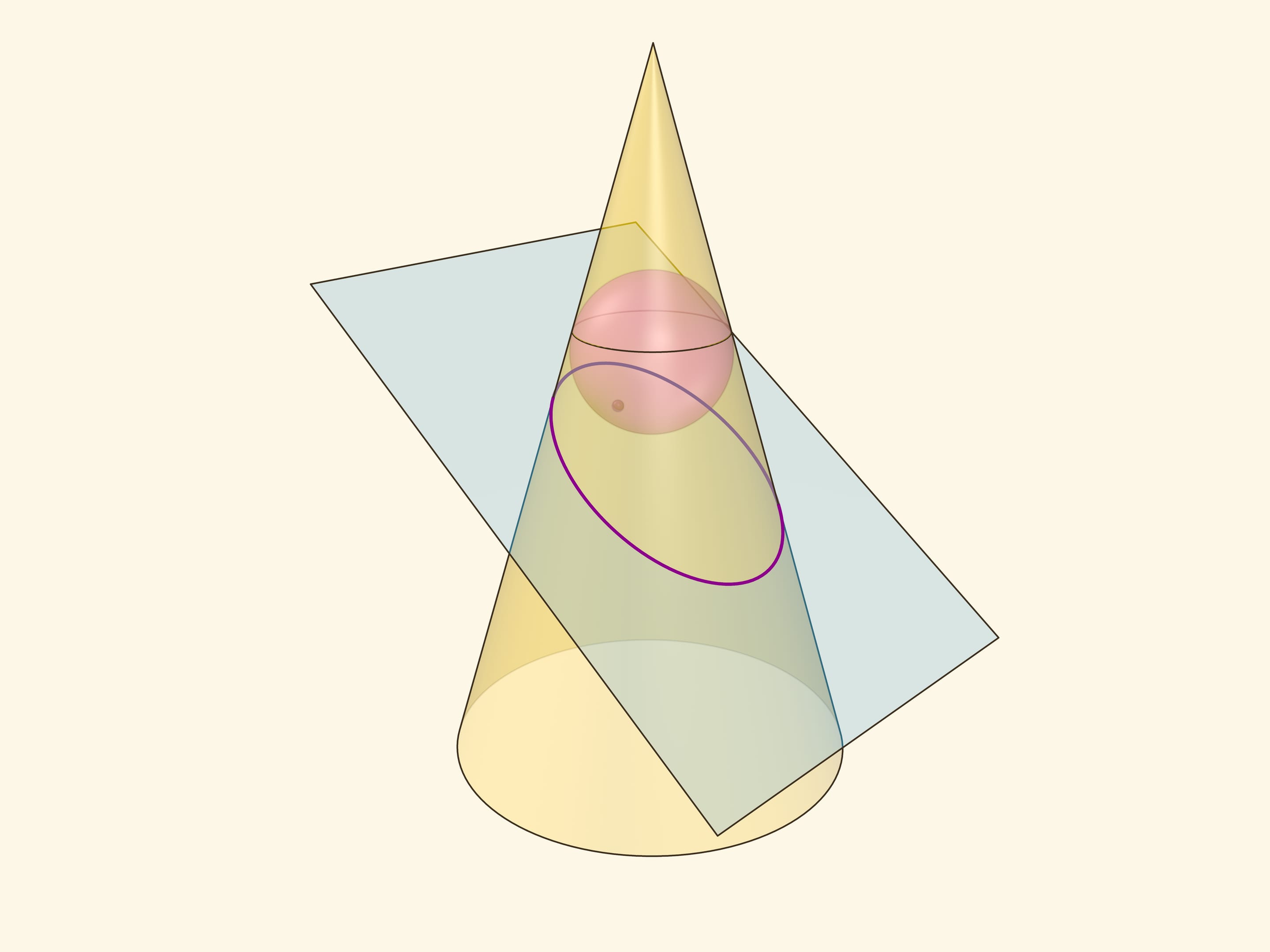
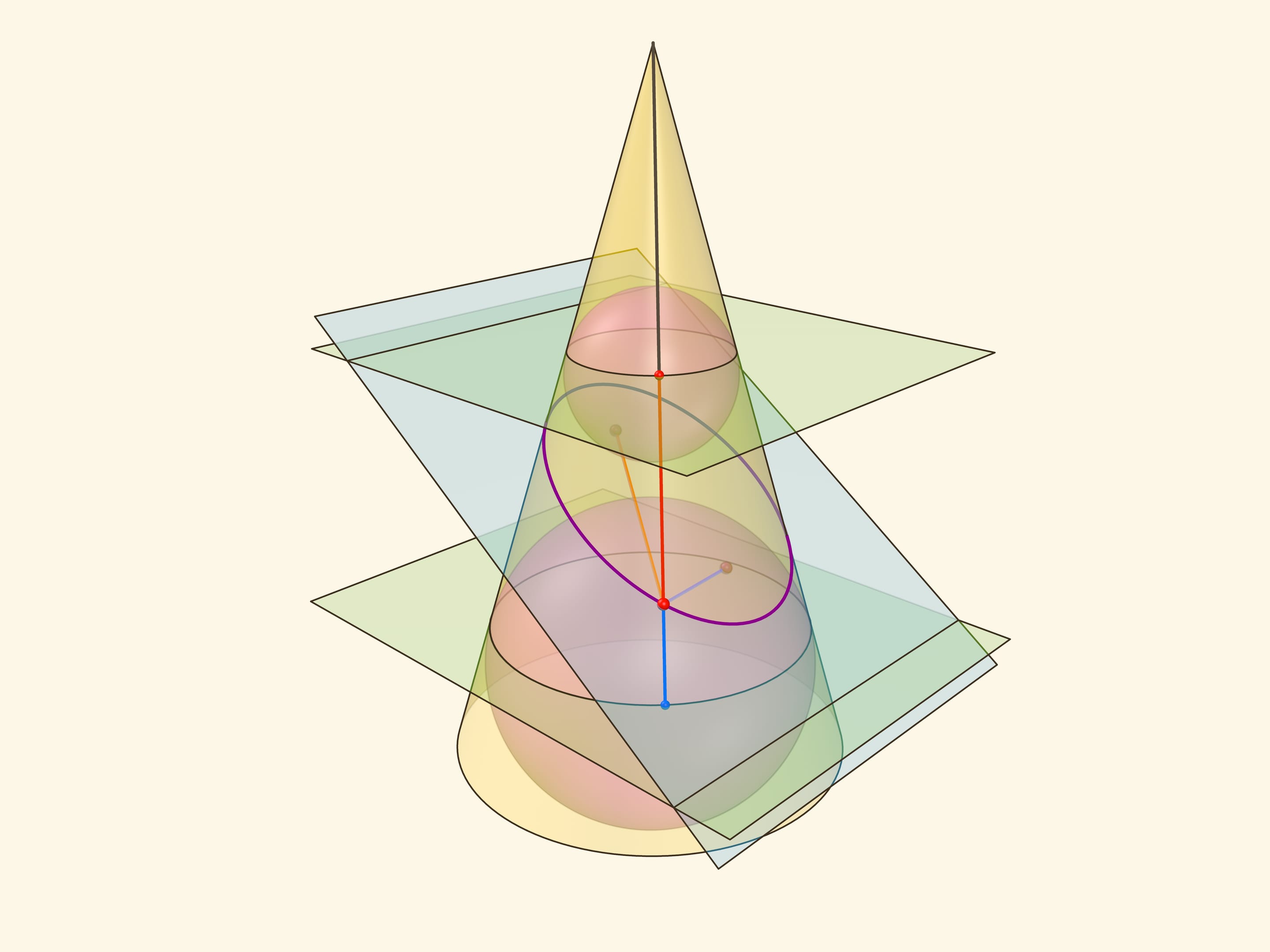
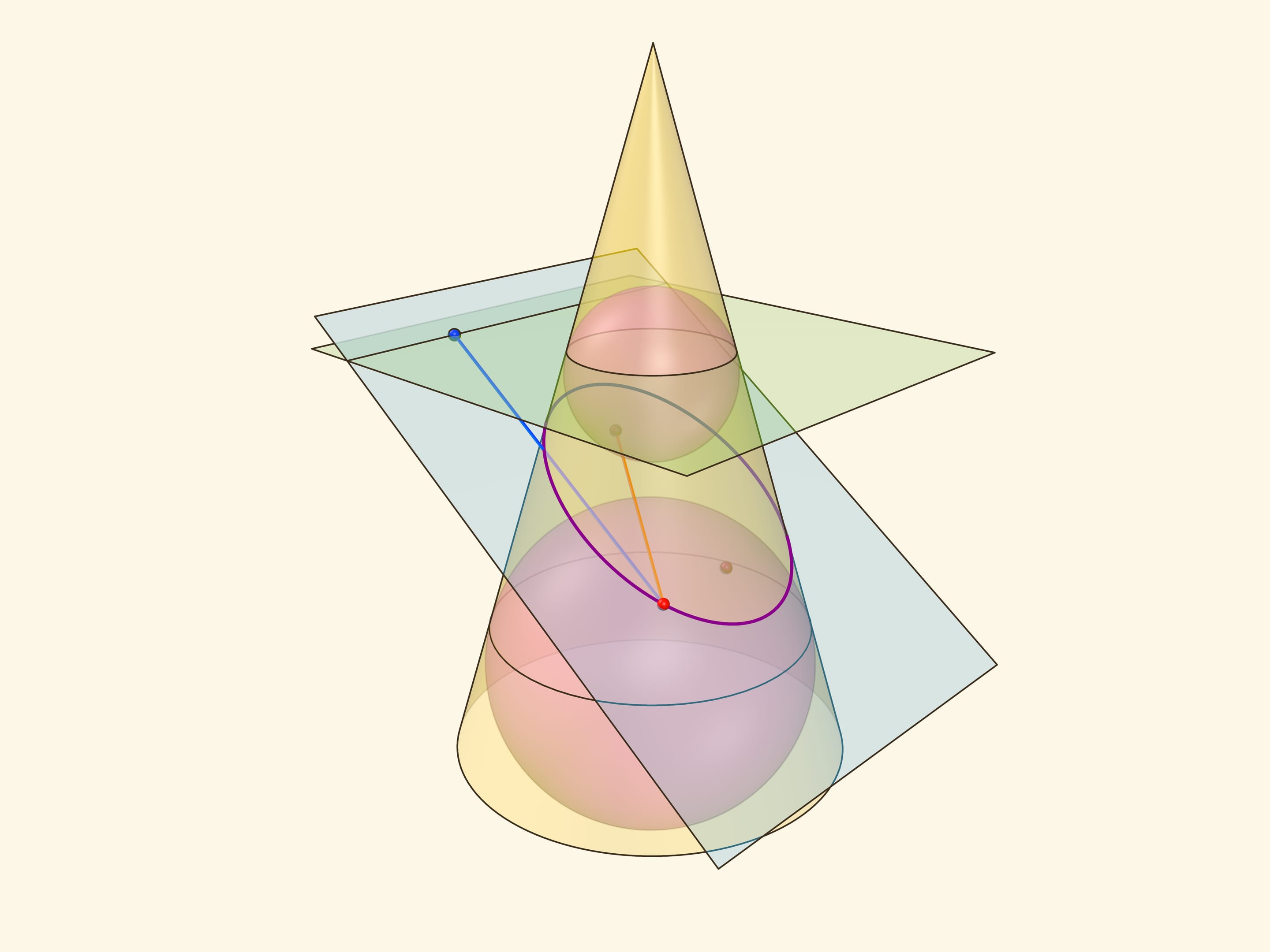
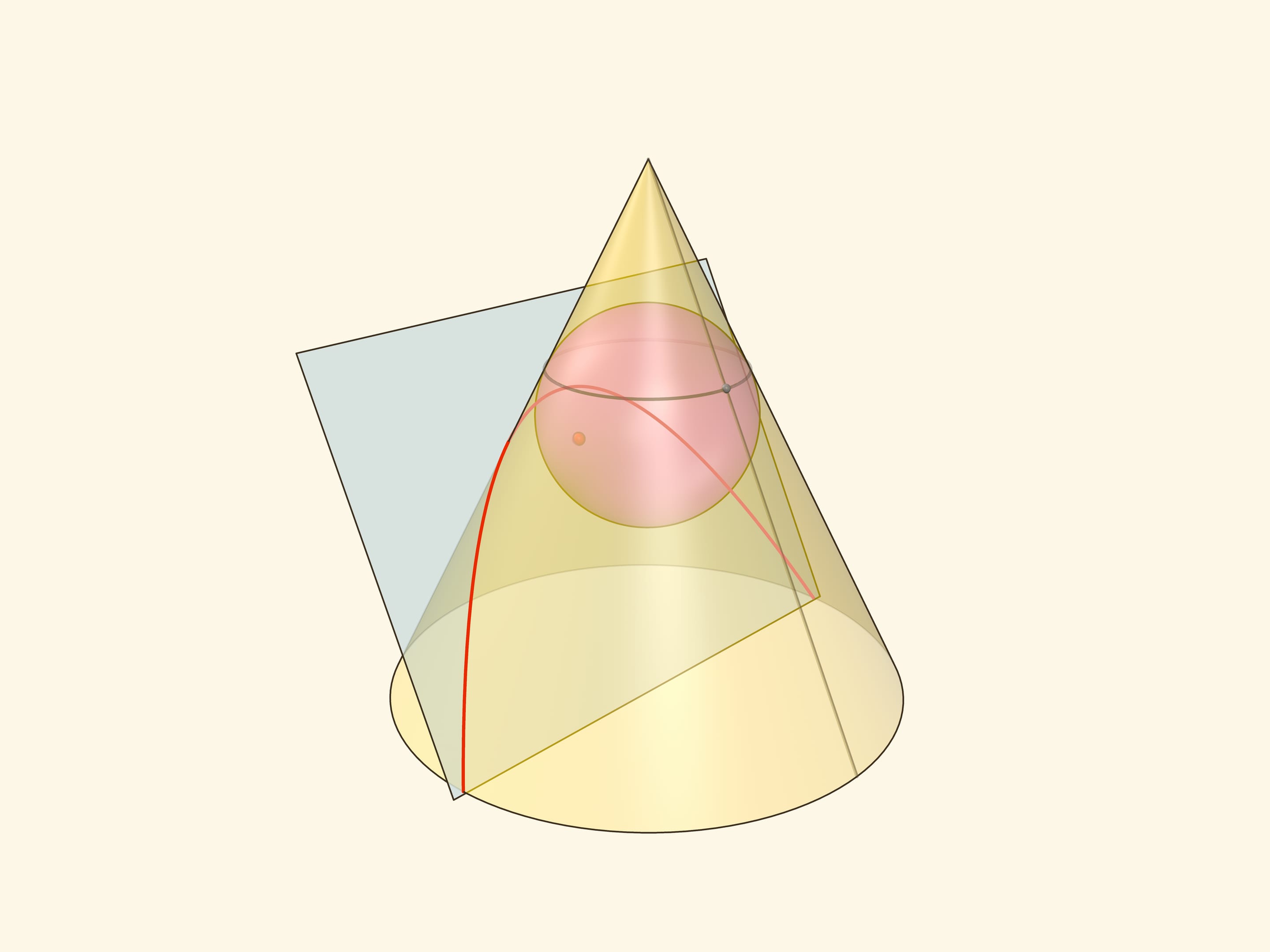
Аналогичные рассуждения проходят, если определять эллипс как сечение конуса плоскостью, пересекающей все его образующие и не проходящей через его вершину.
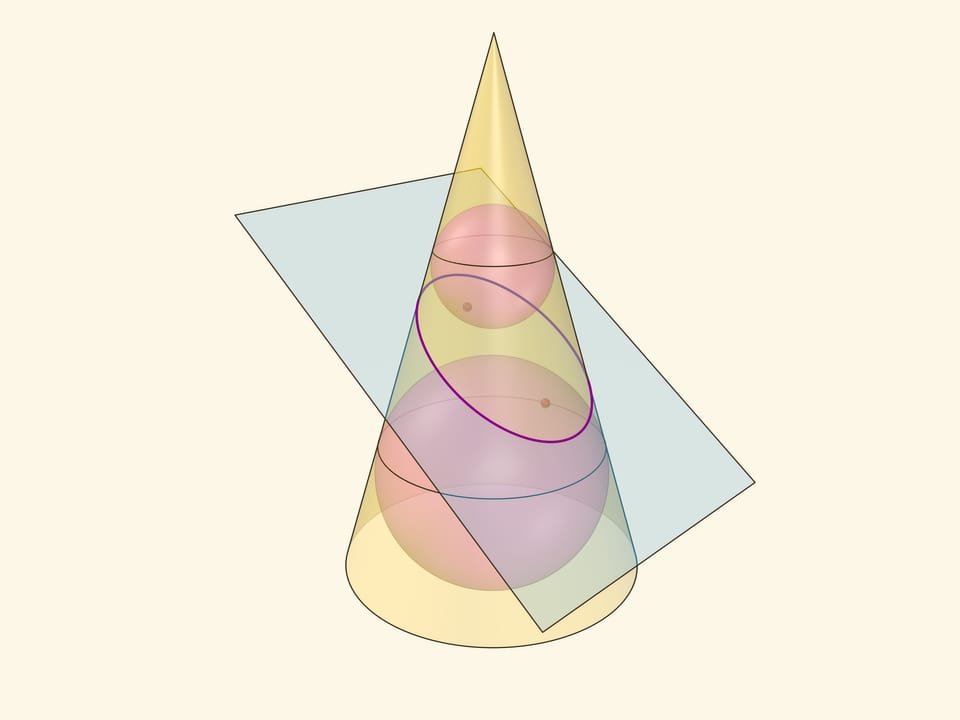
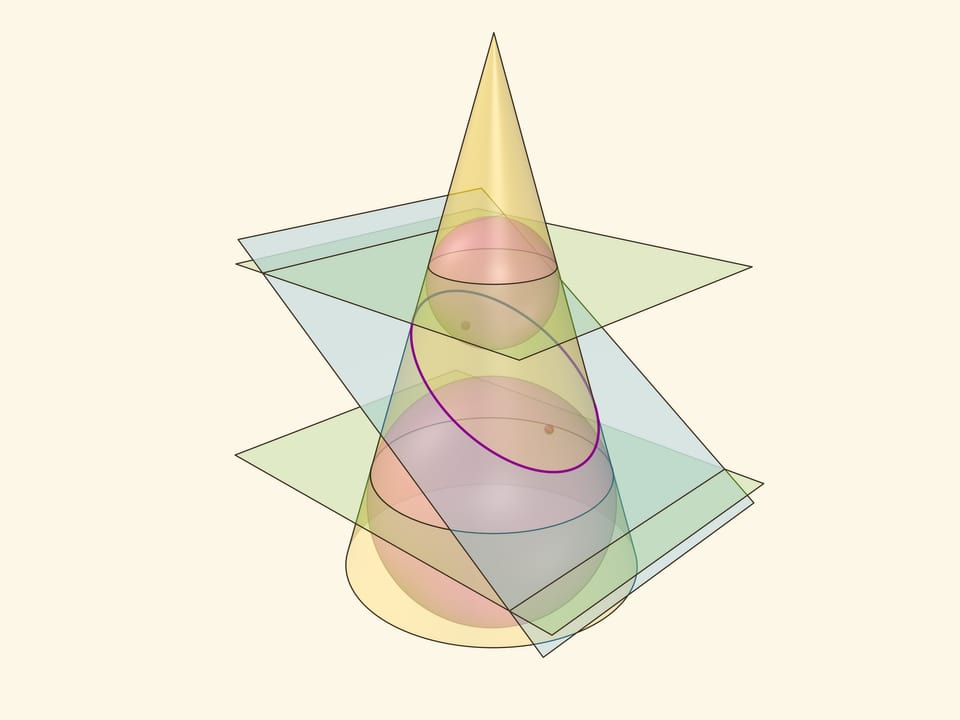
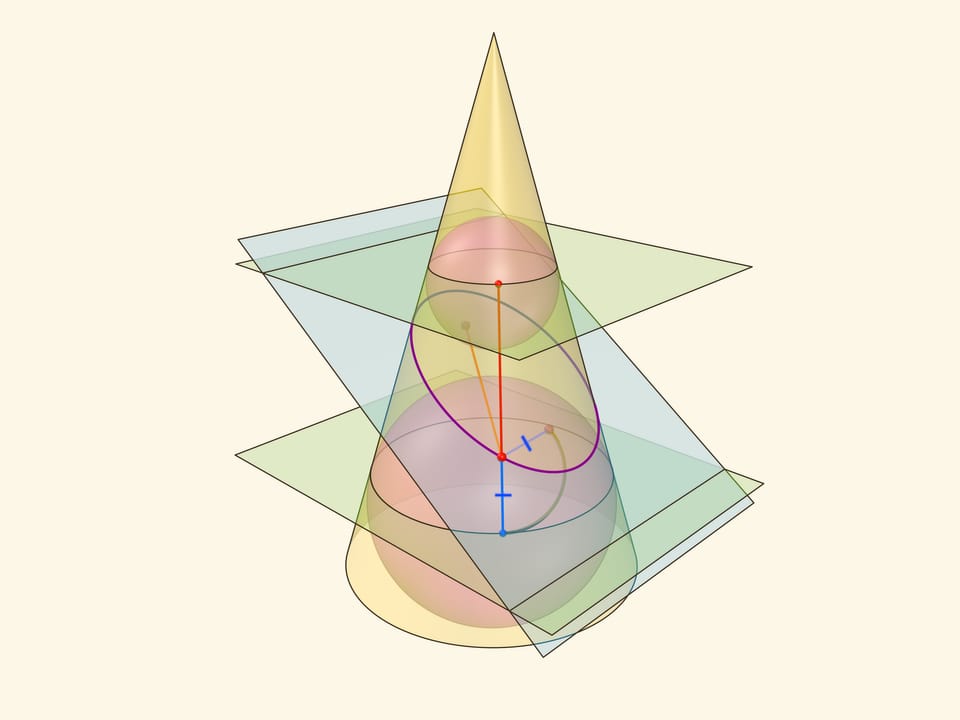
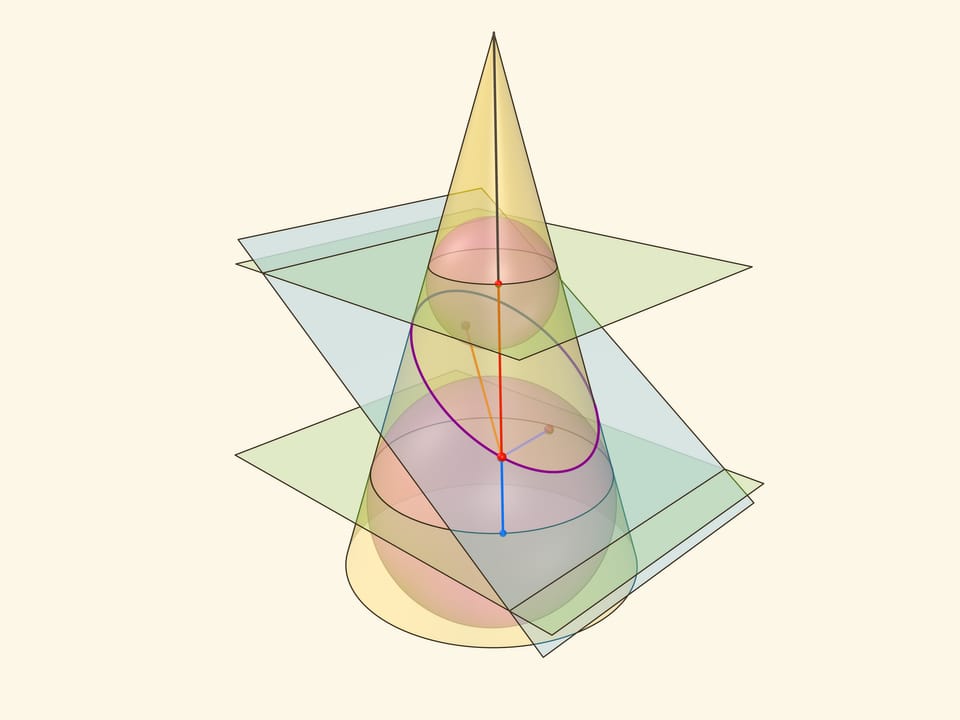
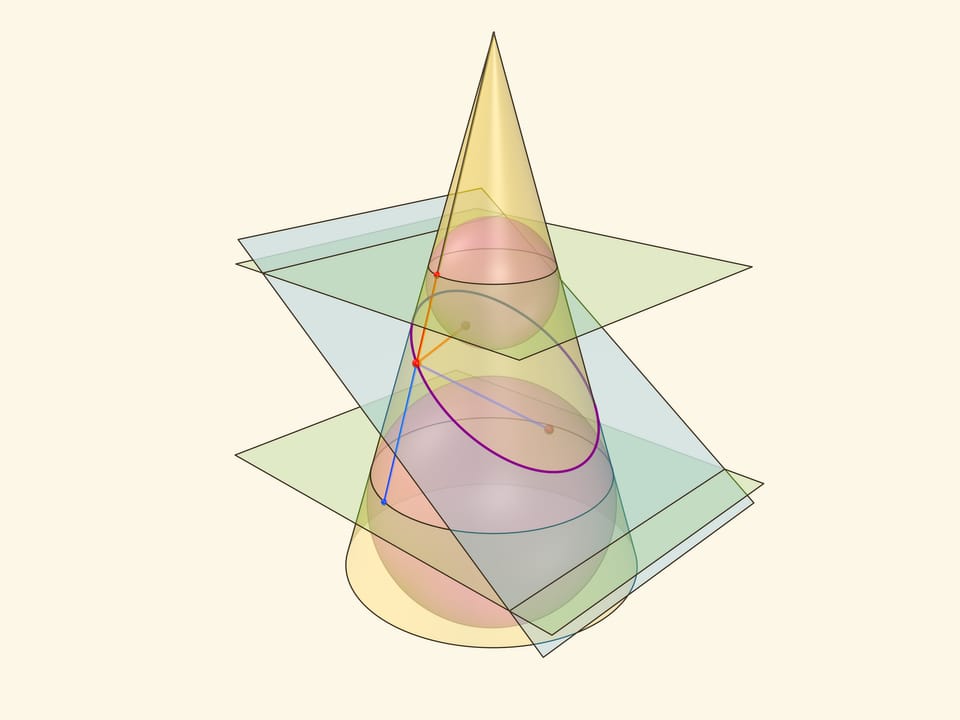
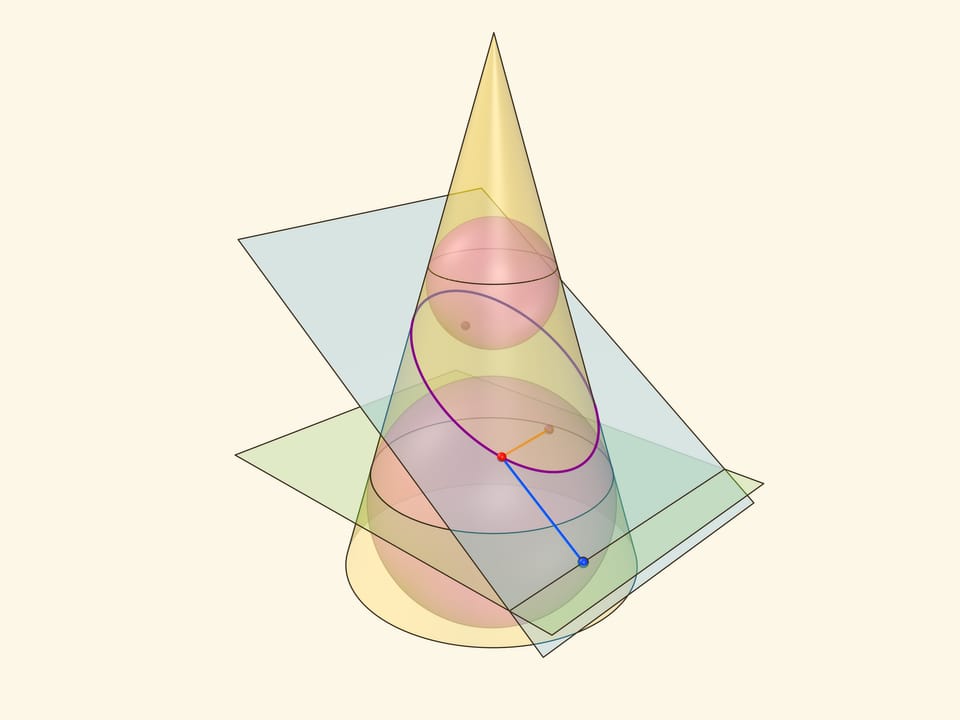
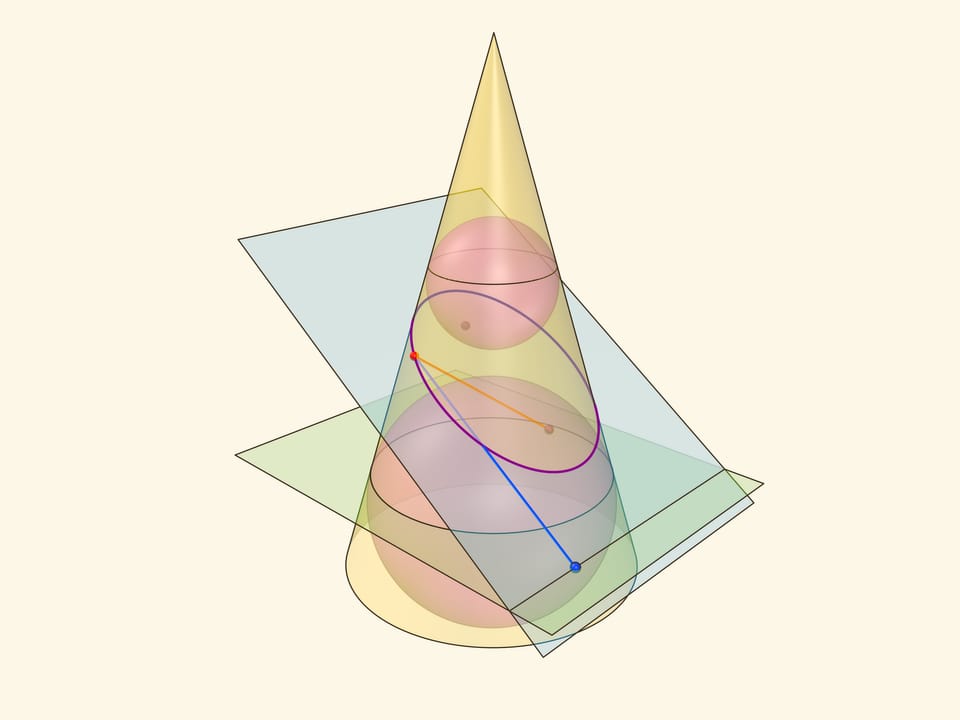
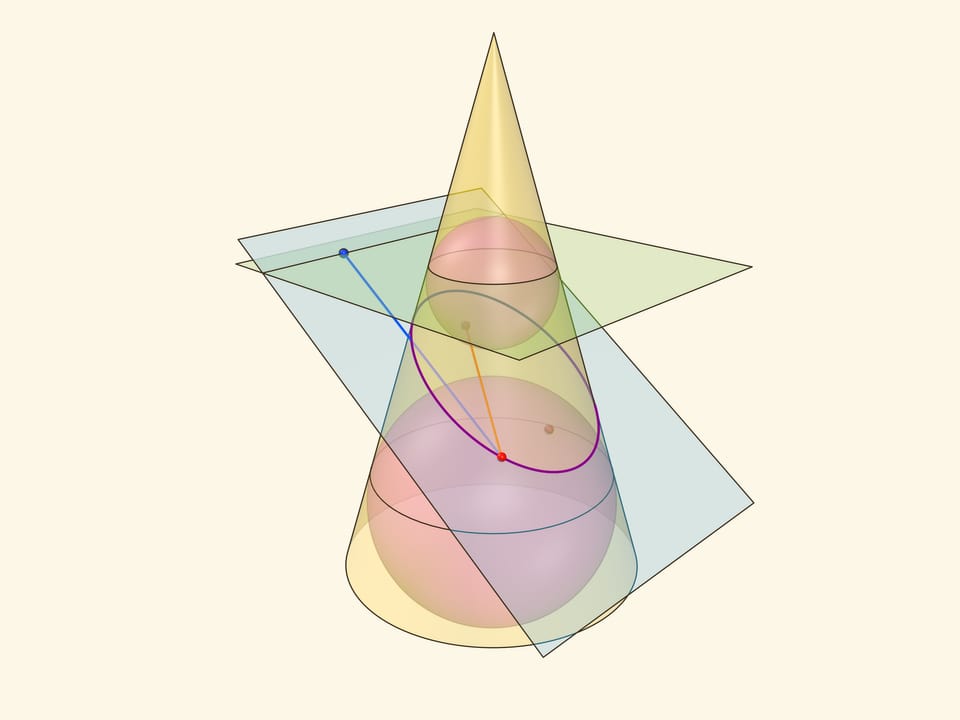
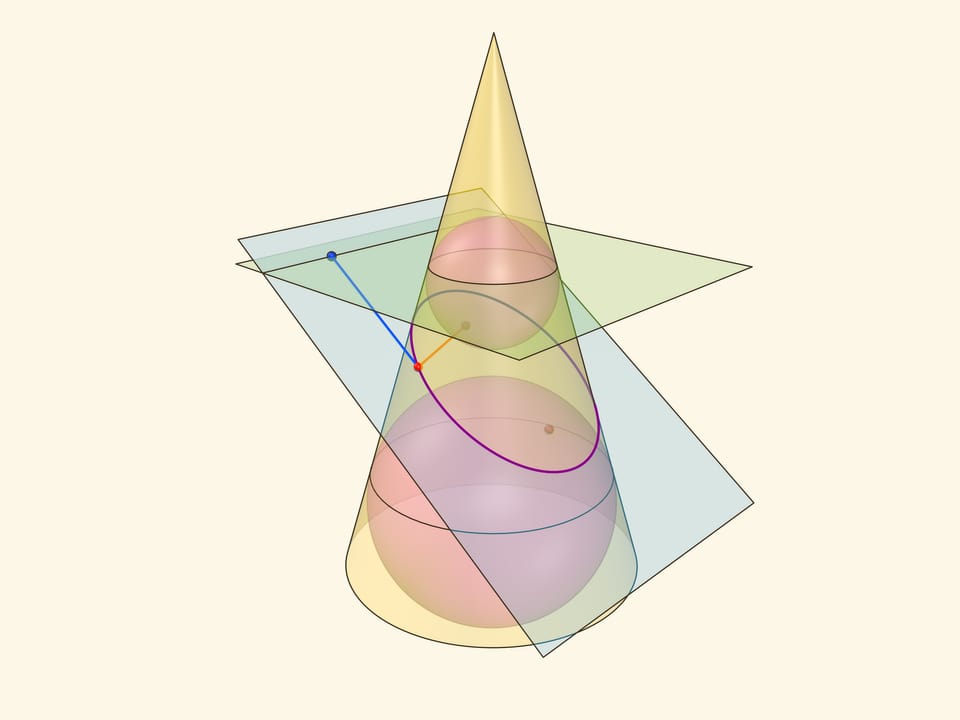
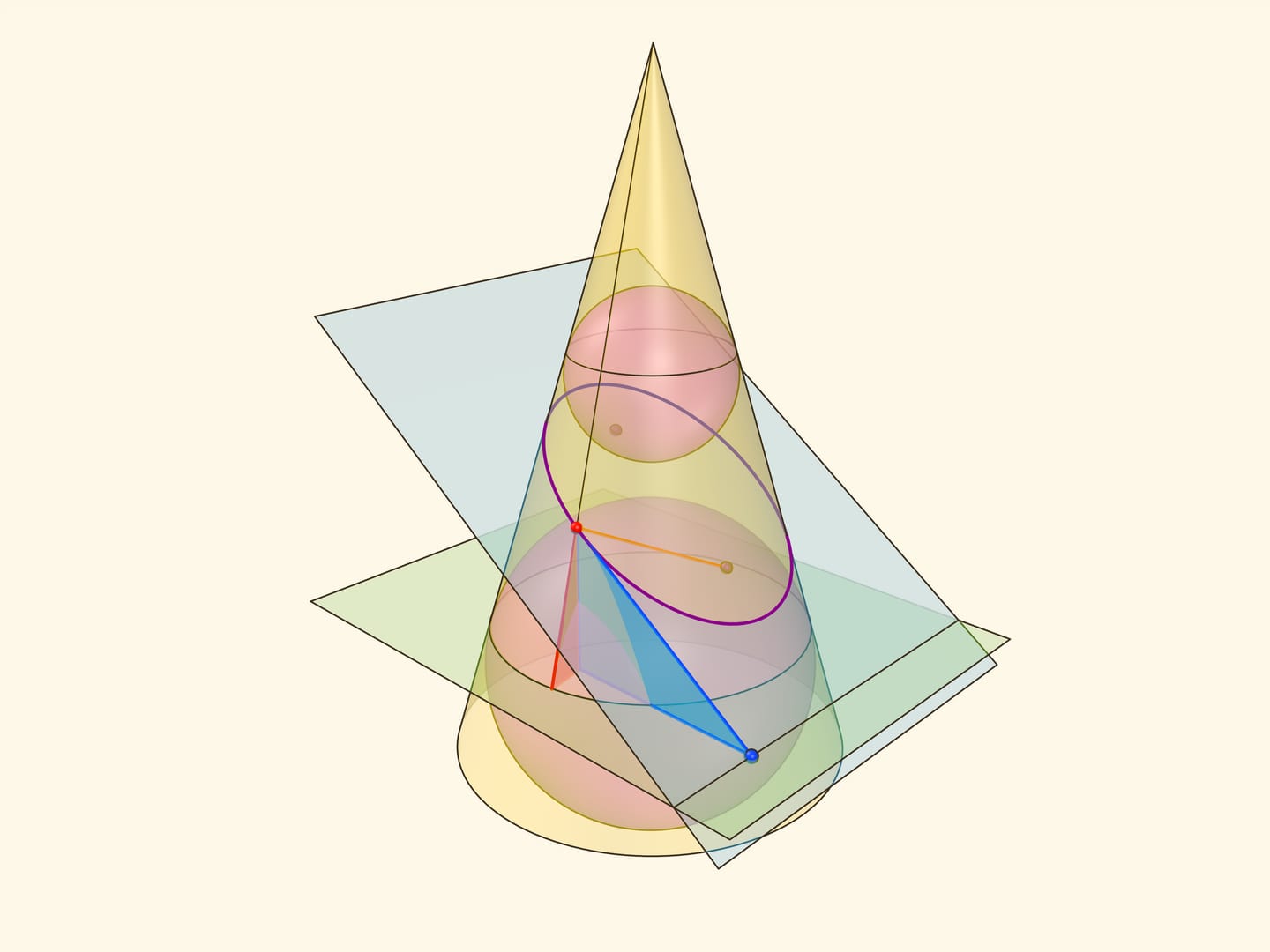
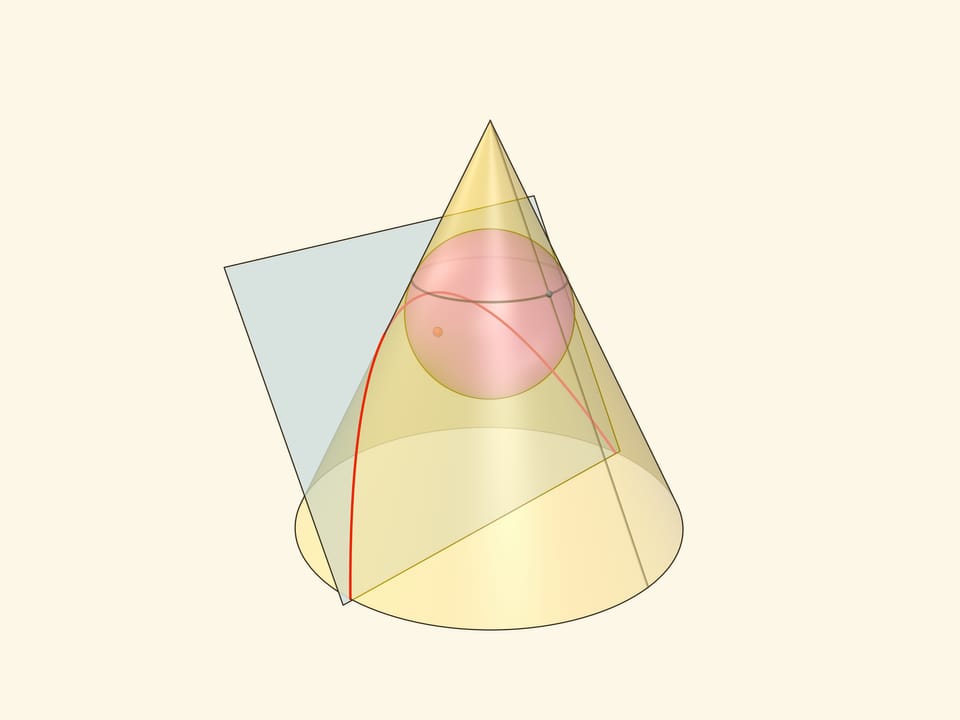
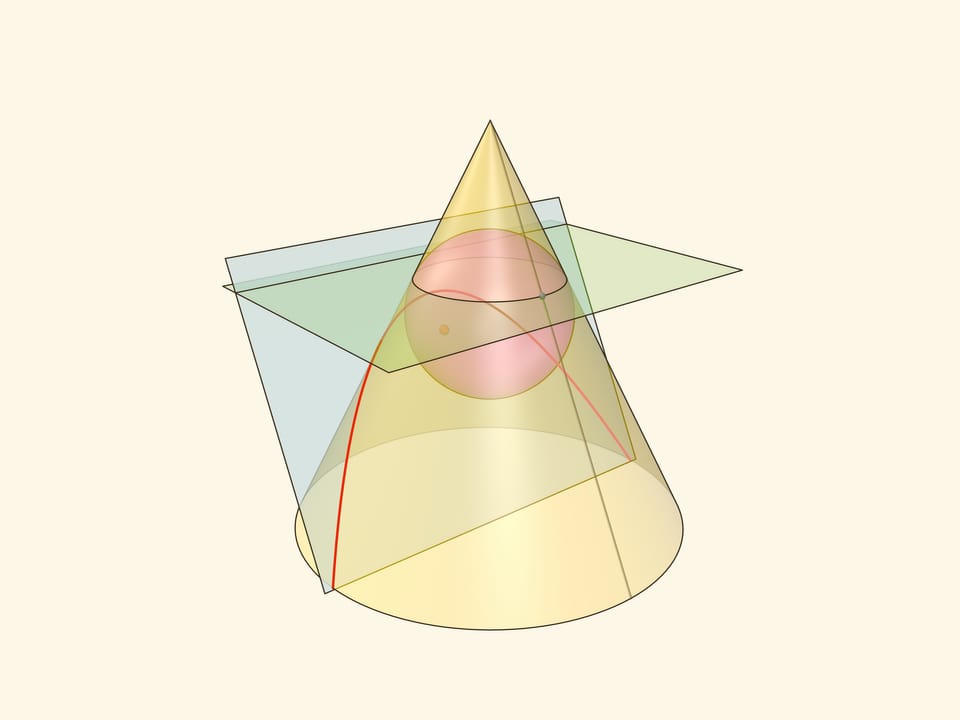
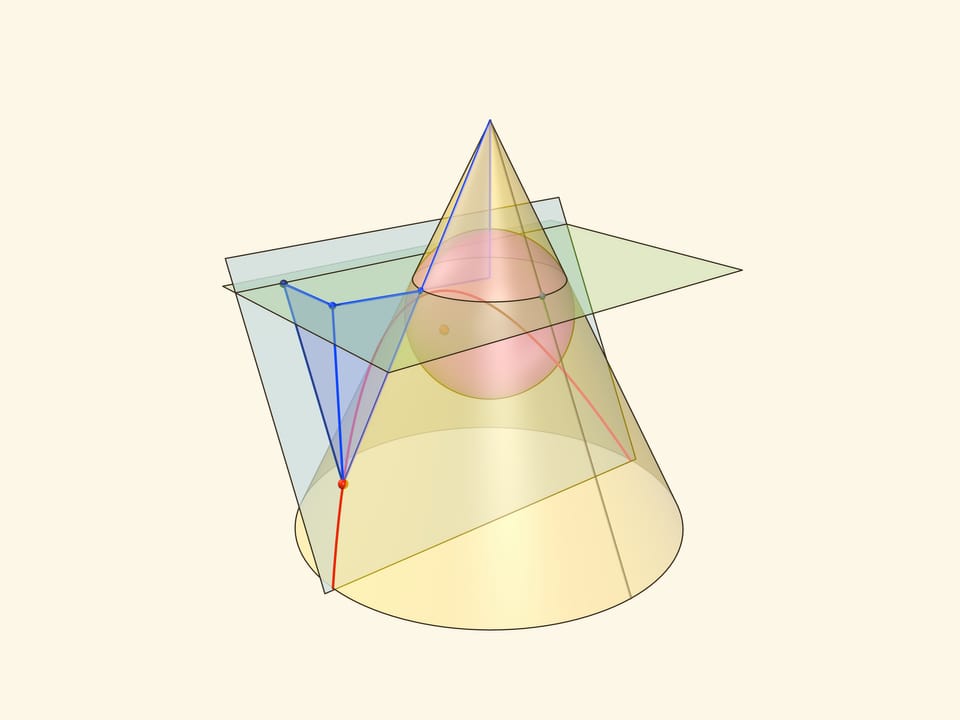
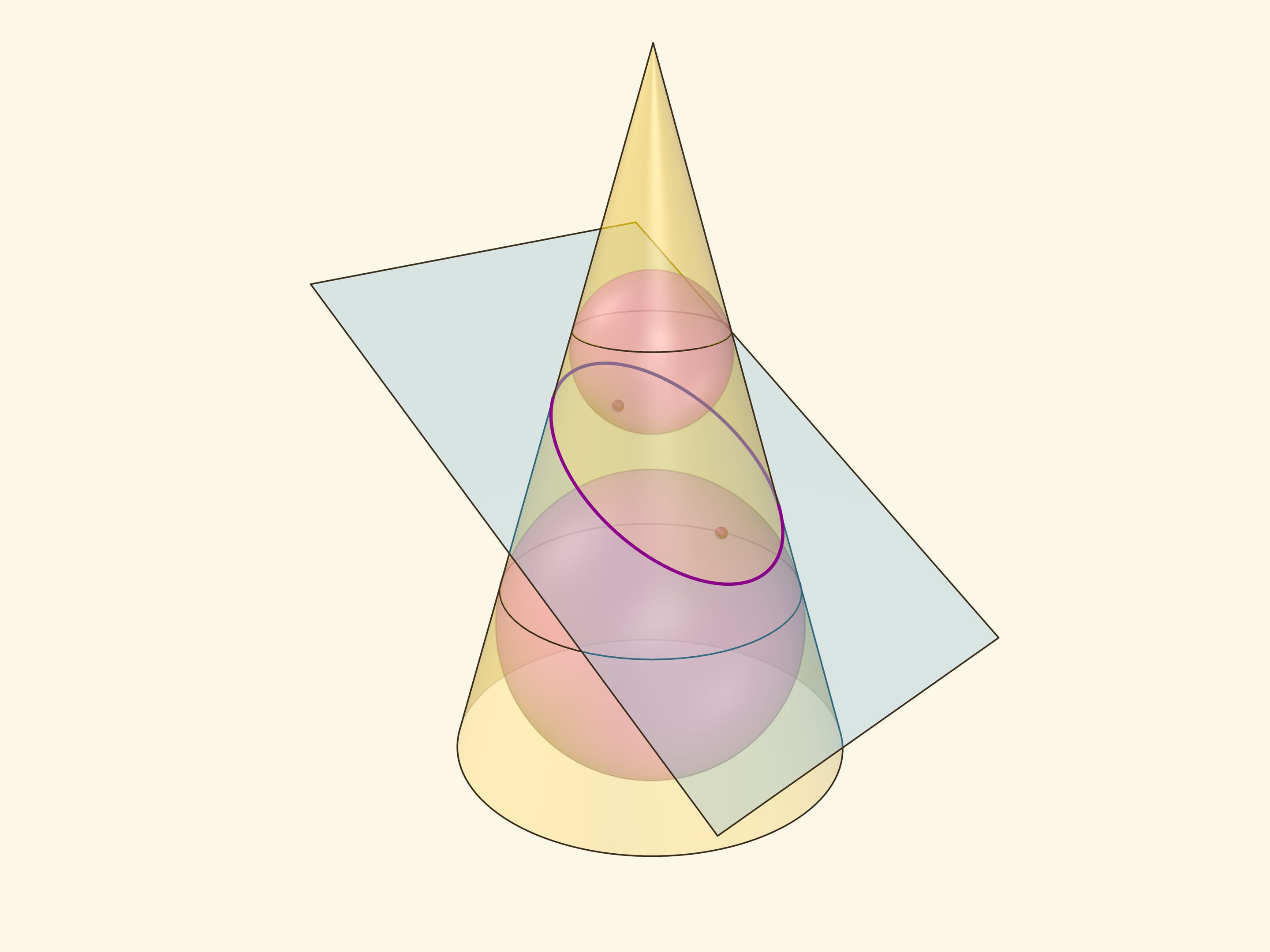
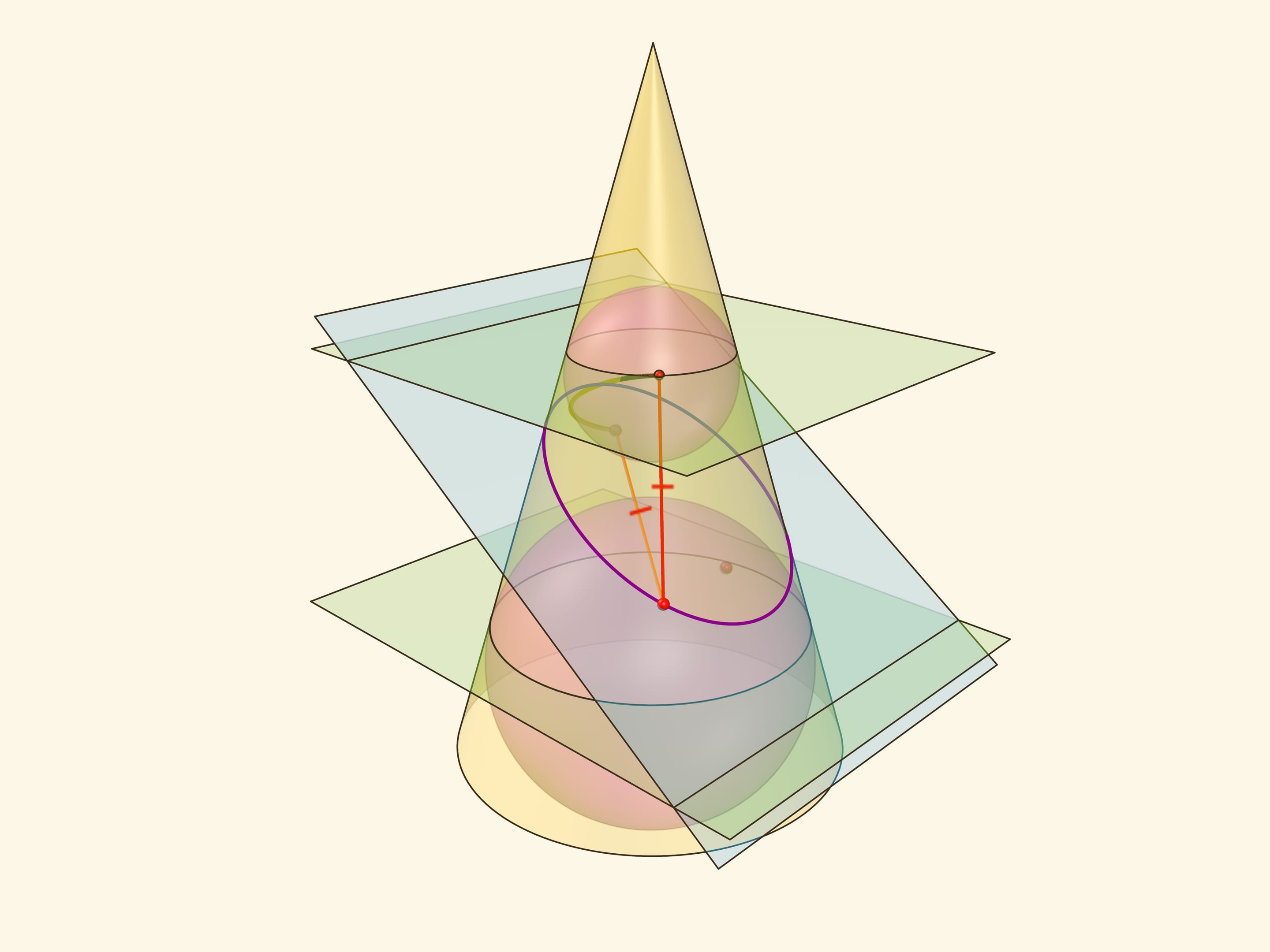
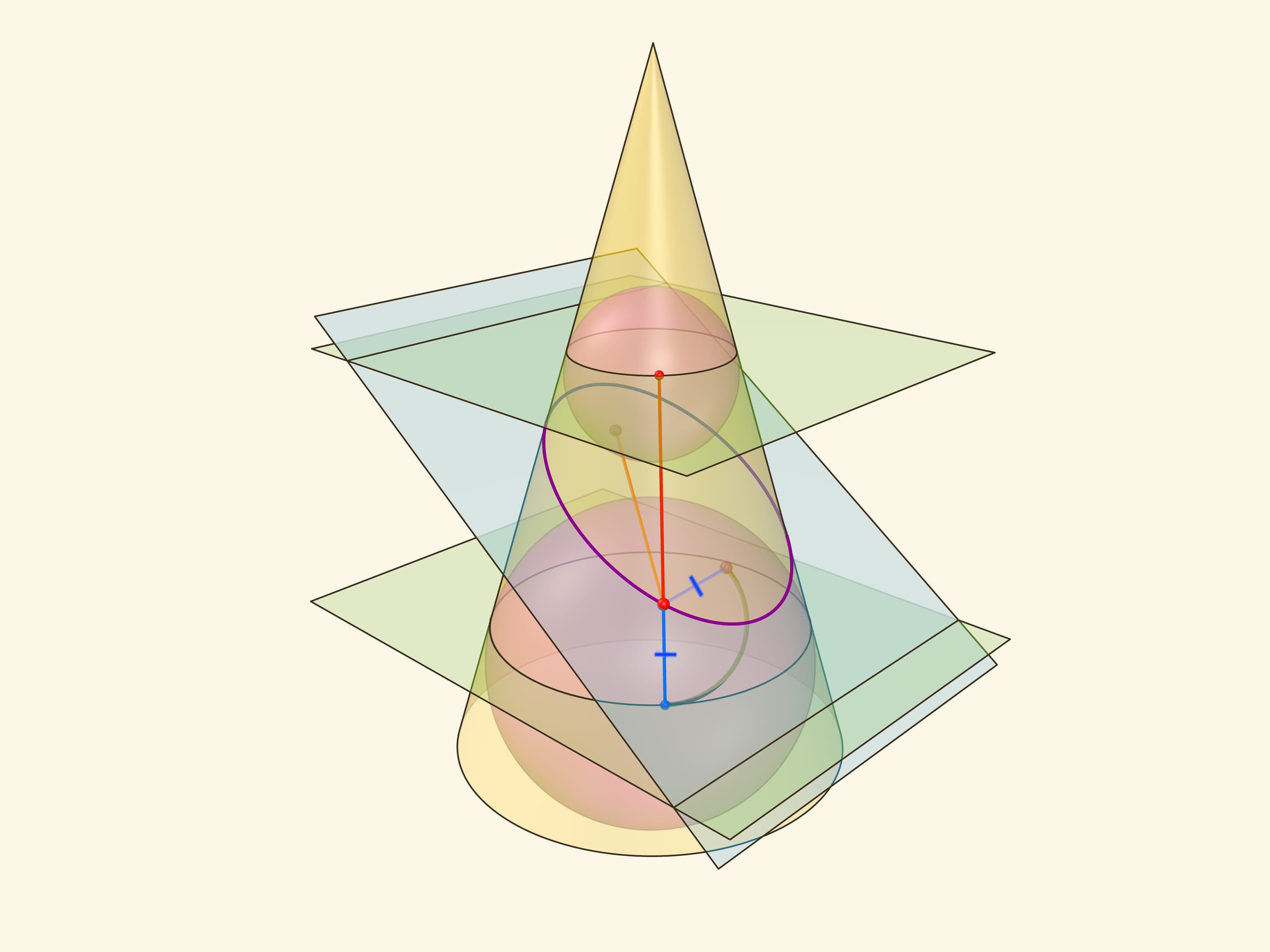
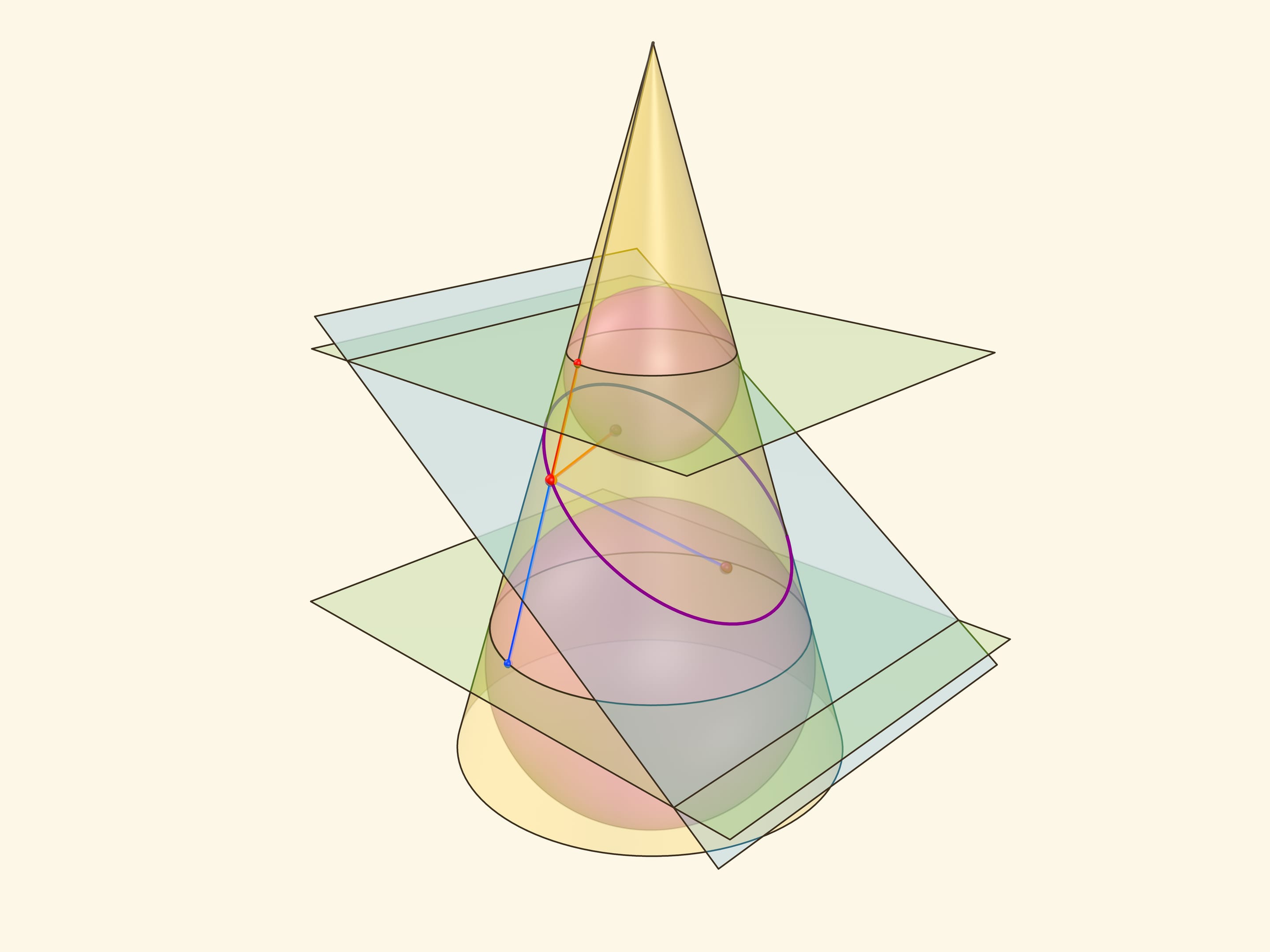
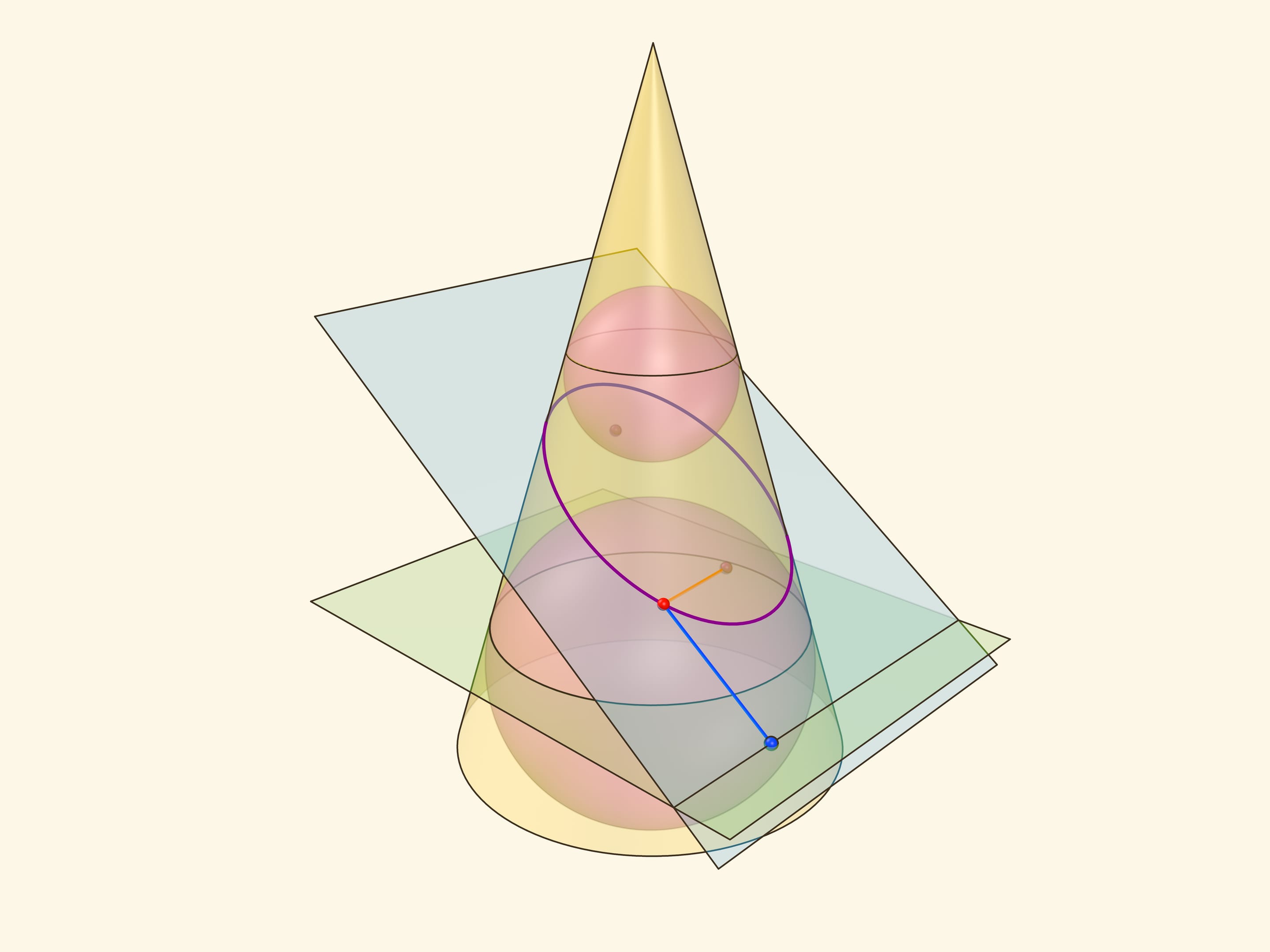
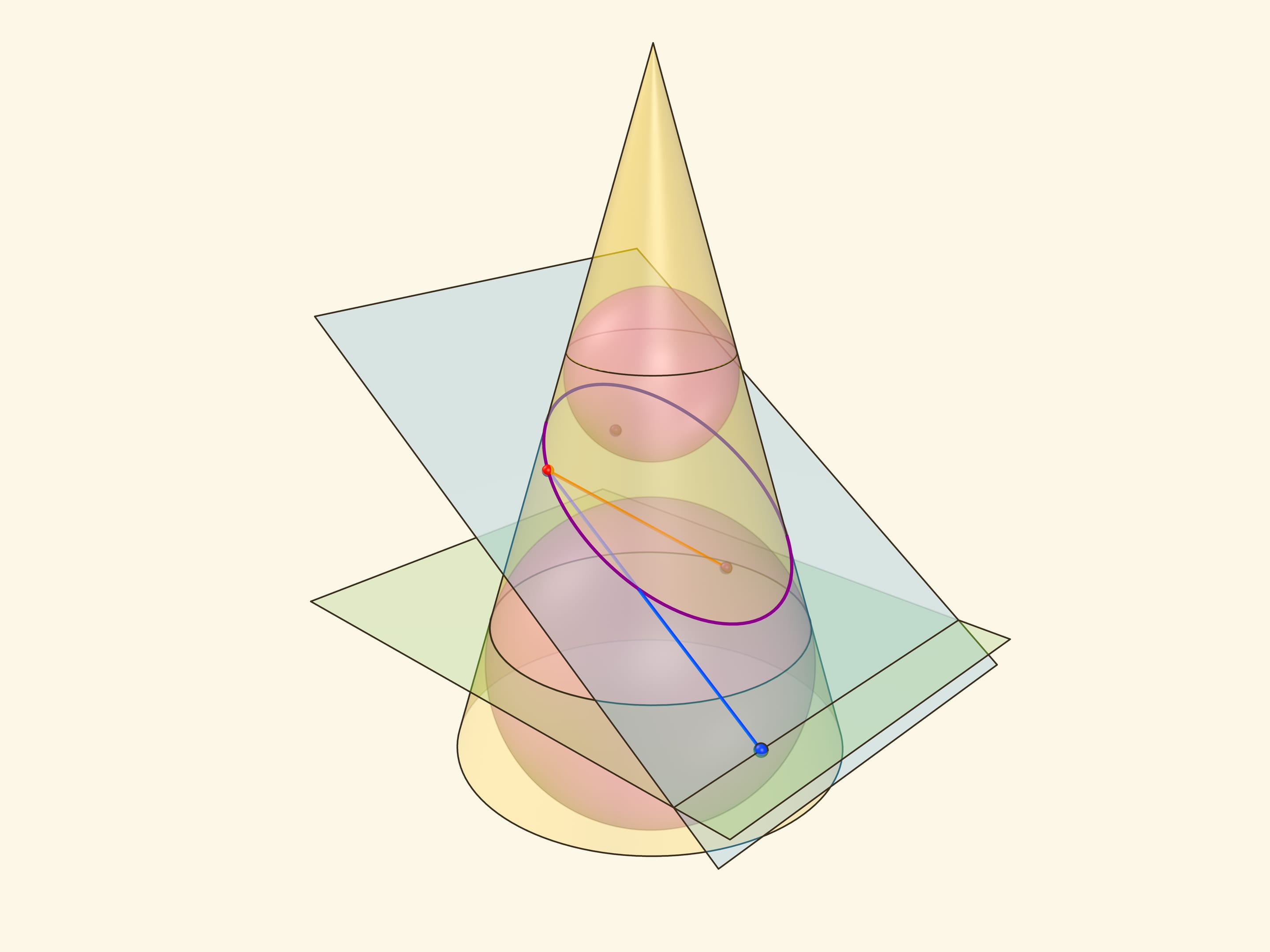
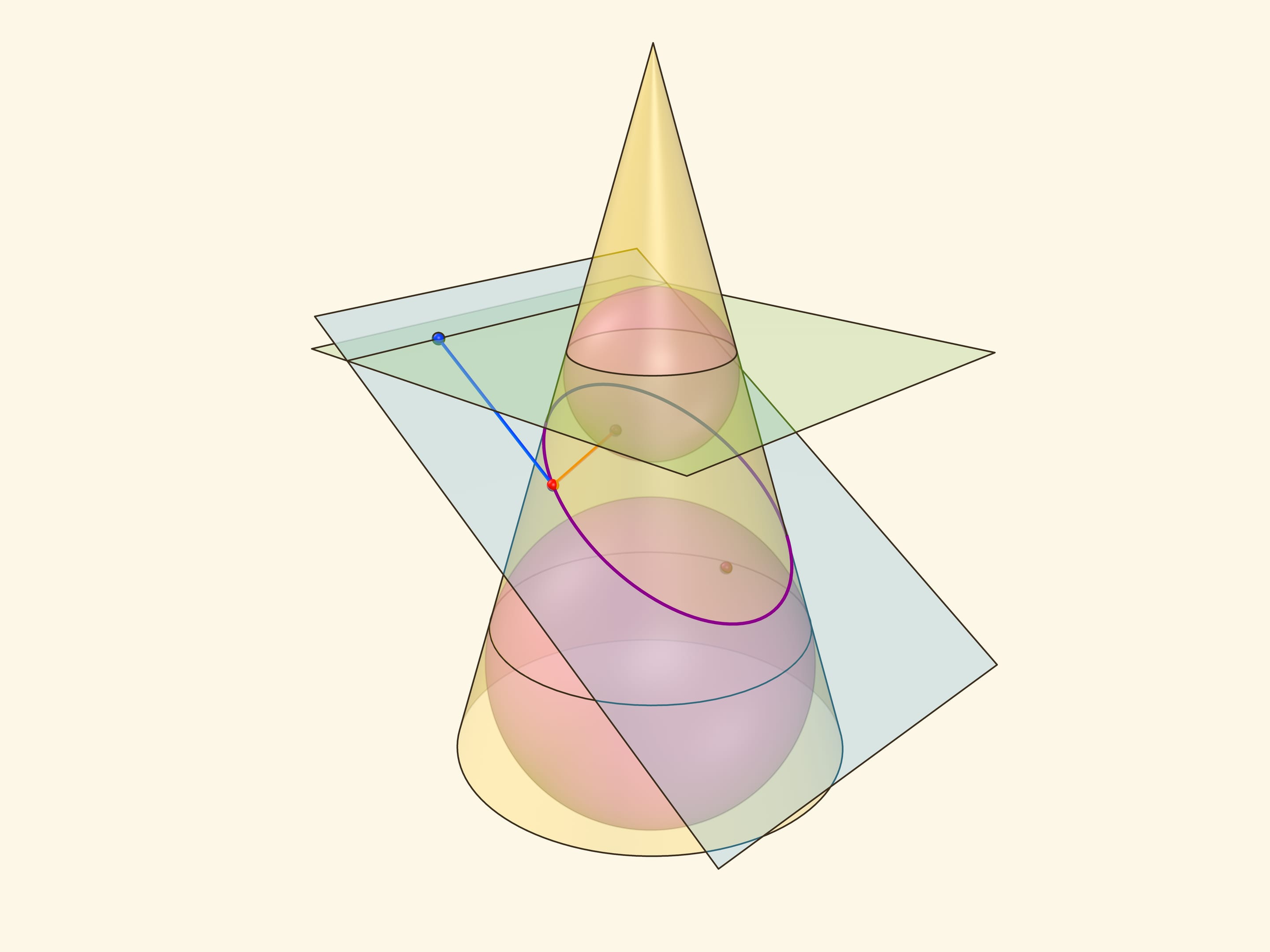
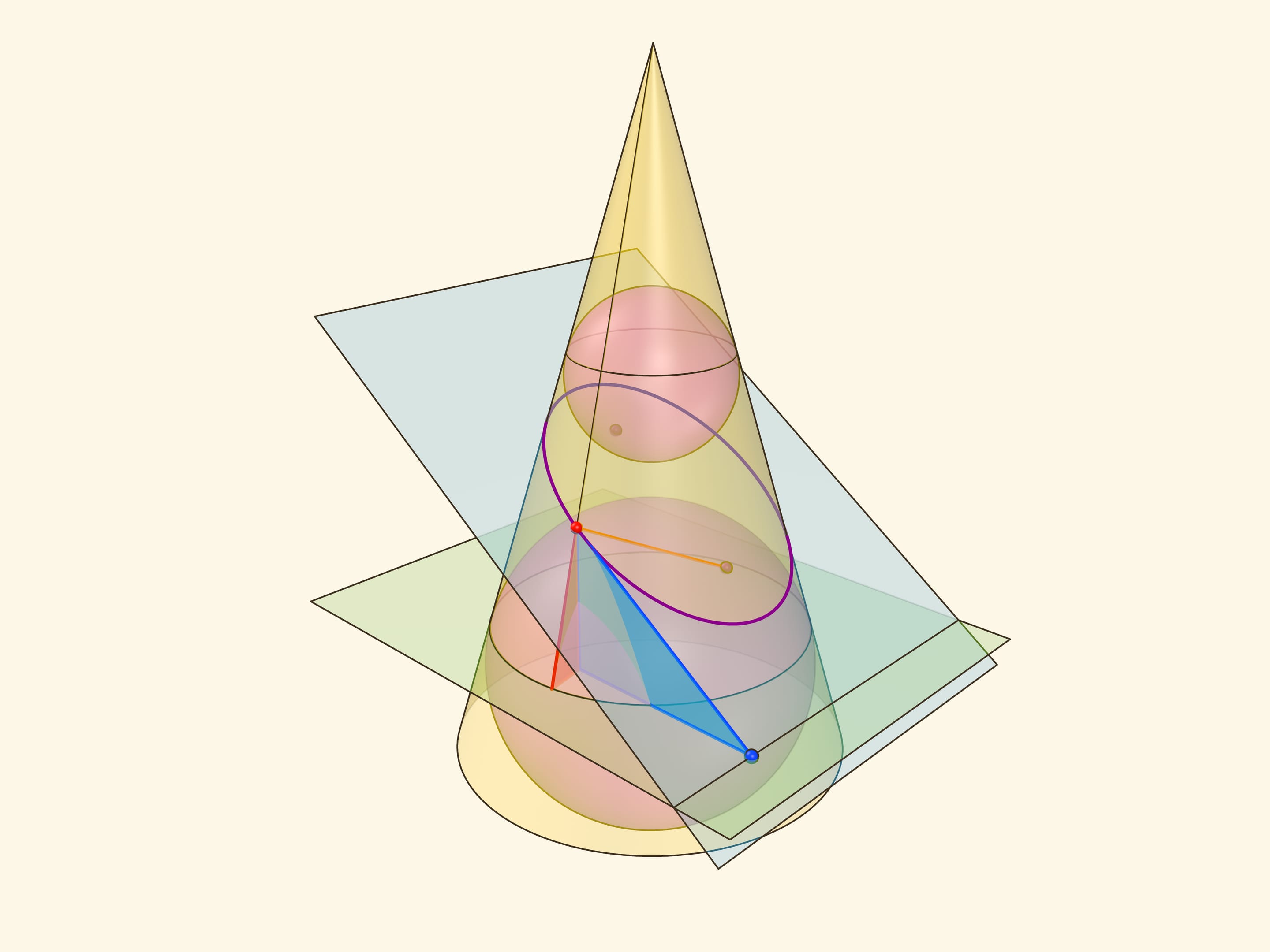
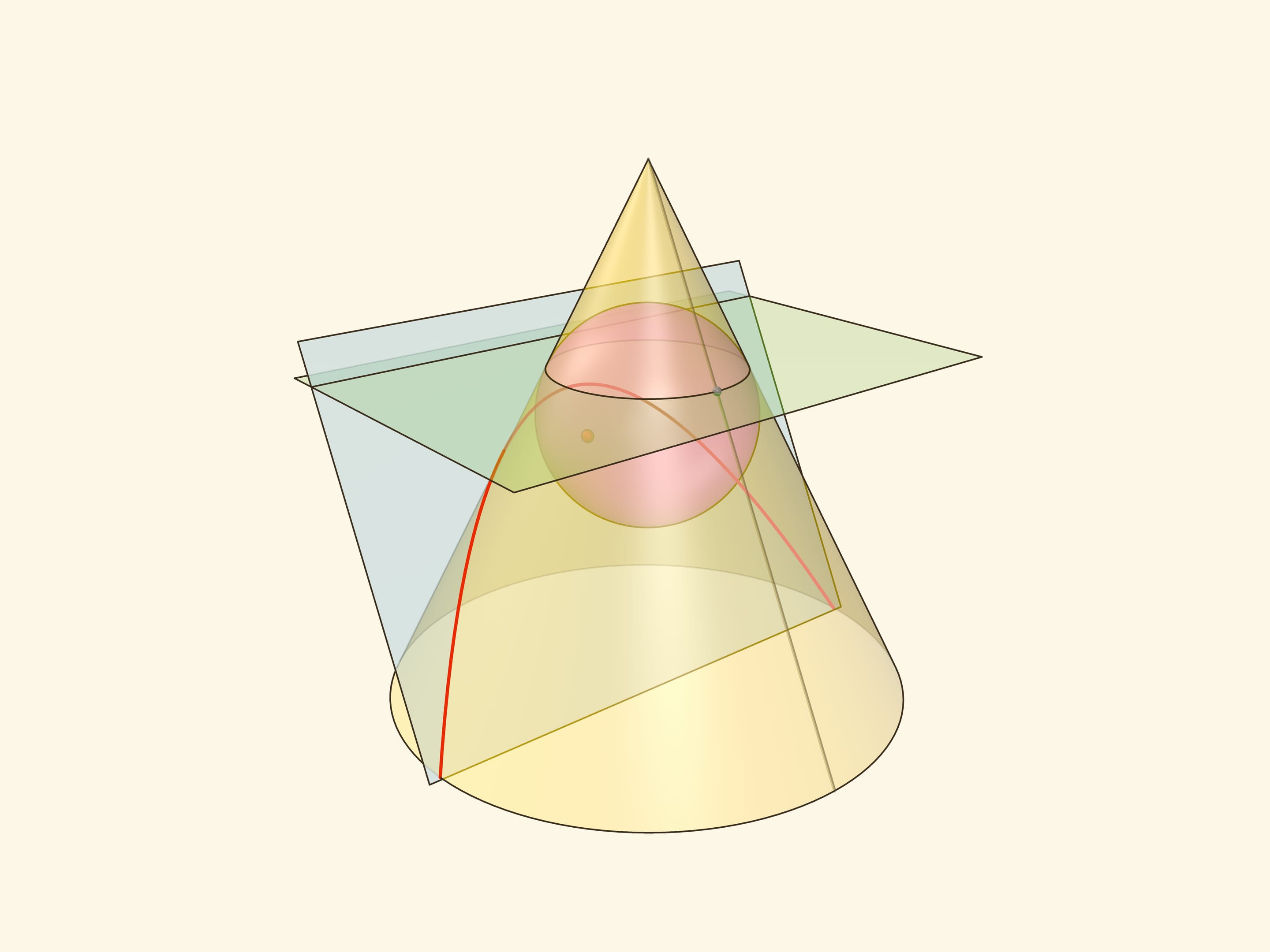
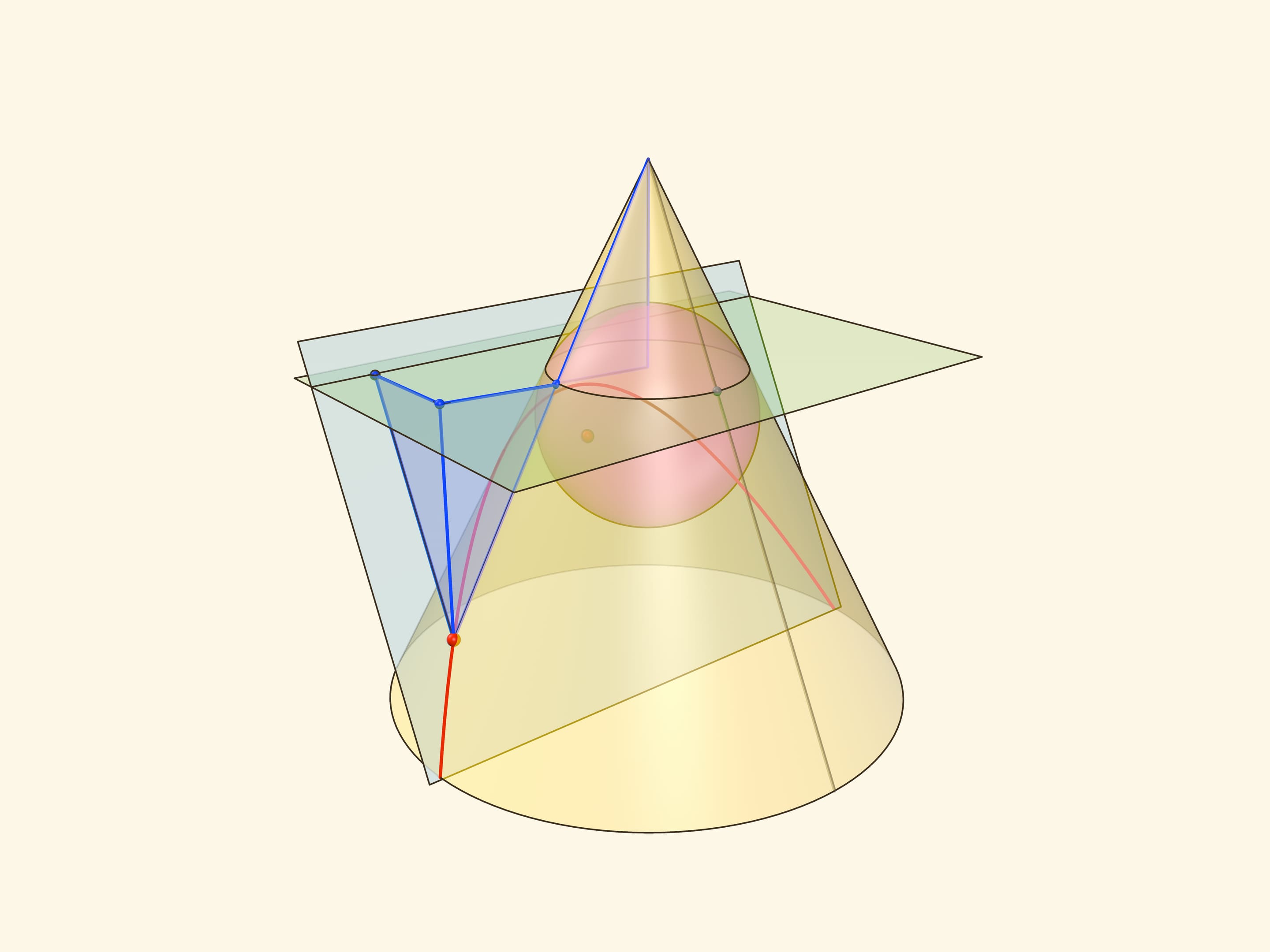
В конус выше и ниже плоскости сечения вписываются шары, которые «раздуваются» до касания с плоскостью. В момент касания это сферы Данделена, а точки касания — фокусы эллипса. Директрисы эллипса — прямые пересечения секущей плоскости с плоскостями, проходящими через окружности касания сфер Данделена и конуса.
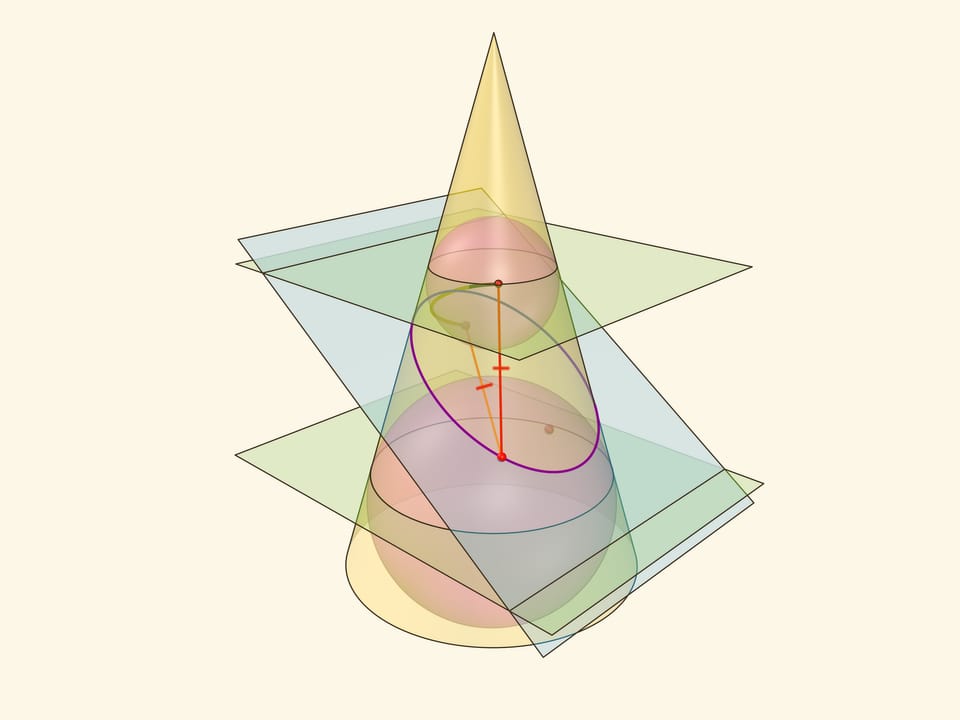
Сумма расстояний от произвольной точки эллипса до фокусов равна длине отрезка образующей конуса, заключённой между «горизонтальными» плоскостями.
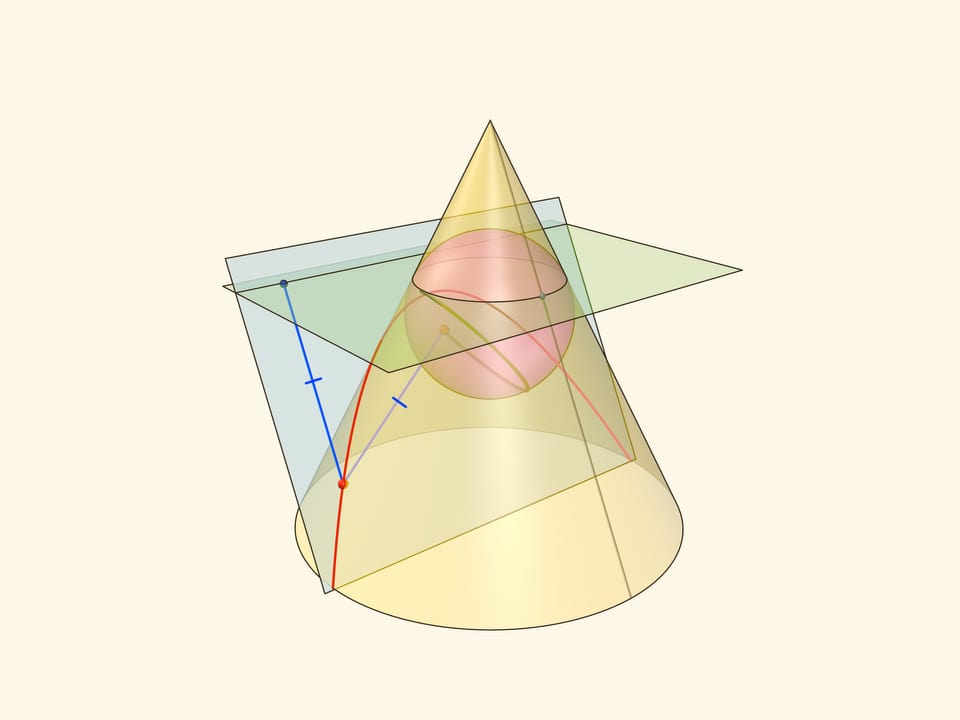
Эксцентриситет эллипса — отношение расстояния от точки эллипса до фокуса к расстоянию от точки до директрисы — не зависит от рассматриваемой точки эллипса и есть величина постоянная, меньше единицы.
Именно в этом месте рассмотрение эллипса как конического сечения чуть сложнее, чем рассмотрение как сечения цилиндра, где возникал «вертикальный» прямоугольный треугольник, отношение катета к гипотенузе в котором равнялось эксцентриситету. Образующая конуса наклонена к горизонтальной плоскости и аналог того треугольника уже не будет прямоугольным. Приходится рассматривать отношения сторон в двух прямоугольных треугольниках с общим катетом — перпендикуляром, опущенным из точки эллипса на горизонтальную плоскость.
Итак, рассмотрение сфер Данделена даёт определения фокусов и директрис эллипса и позволяет показать, что из определения эллипса как конического сечения следуют геометрическое определение эллипса и определение через эксцентриситет.
Заканчивая рассмотрение эллипса, заметим, что из плоской картинки на плакате, иллюстрирующей определение эллипса через эксцентриситет, сразу следует эквивалентность геометрическому определению: сумма расстояний до фокусов пропорциональна длине отрезка, перпендикулярного двум параллельным директрисам и скользящего вдоль них.
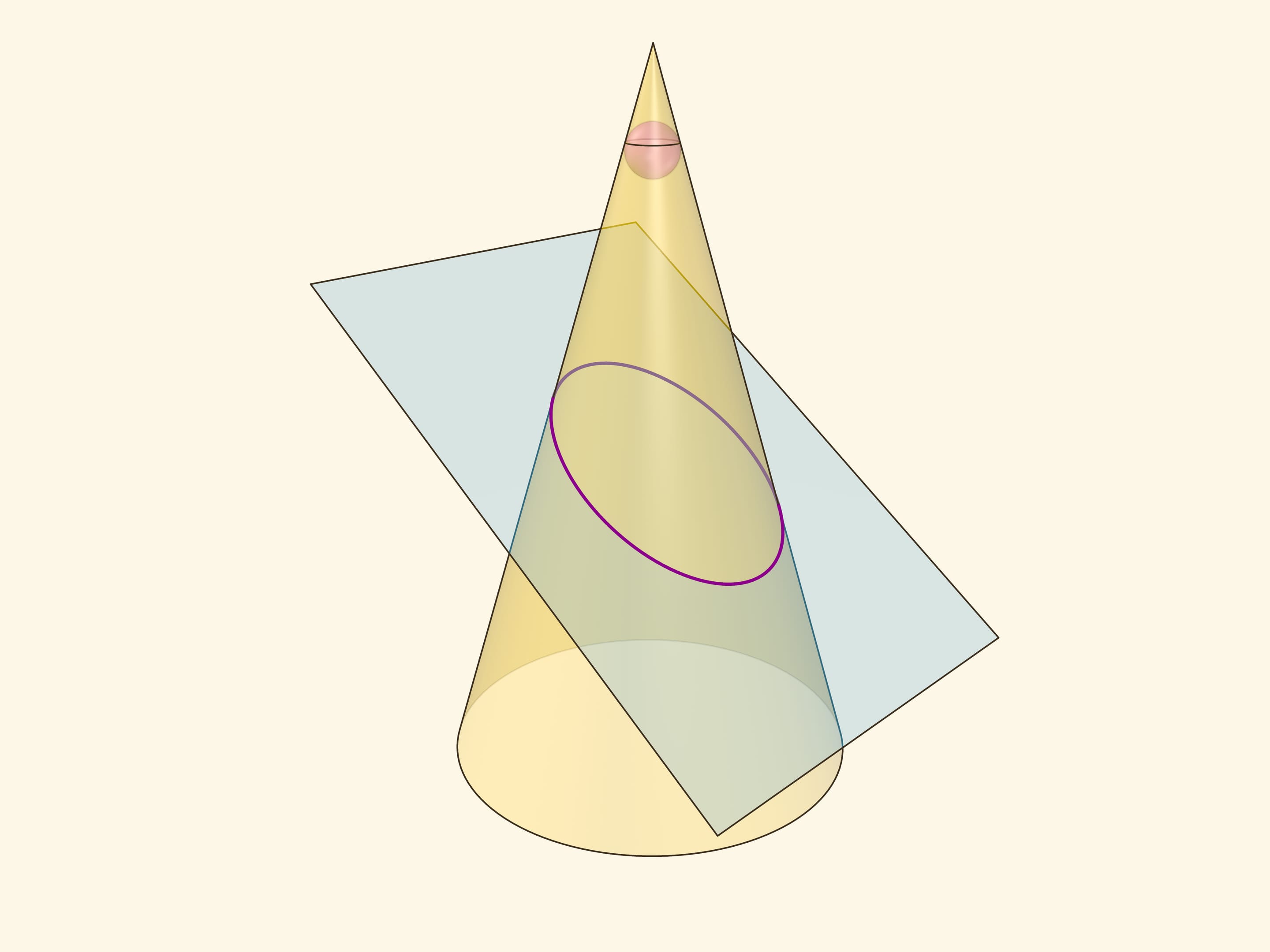
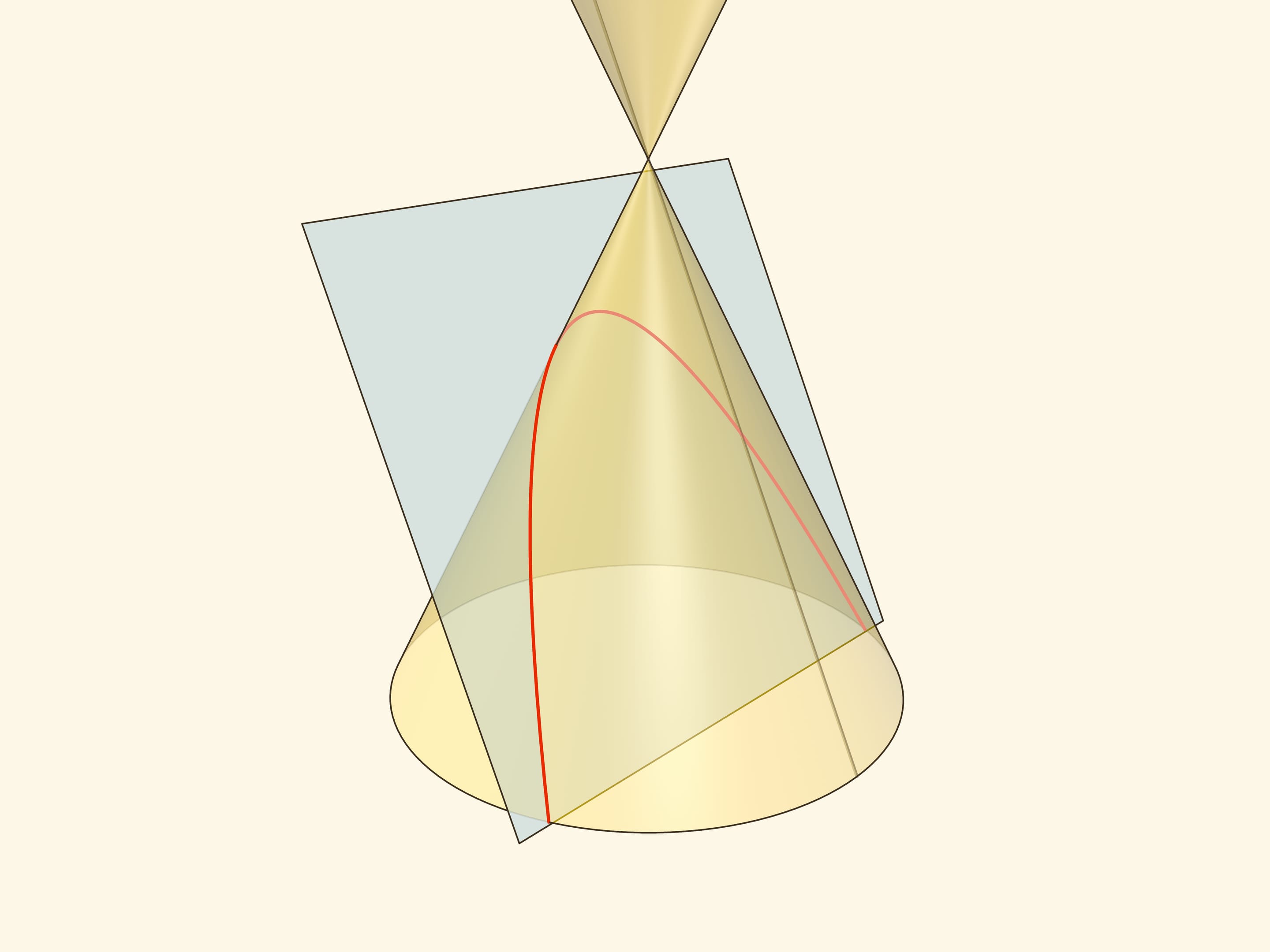
Парабола как коническое сечение возникает, если секущая плоскость параллельна ровно одной образующей конуса (как следствие — пересекается только с одной его полой).
Впишем в конус рядом с вершиной сферу и начнём её раздувать до касания с секущей плоскостью. Точка касания сферы Данделена с секущей плоскостью и есть фокус параболы. В отличие от эллипса и гиперболы у параболы один фокус. Вписать в конус шар «снизу» от так расположенной секущей плоскости невозможно: вписанный шар касается всех образующих конуса, а будучи расположенным ниже плоскости, он не сможет коснуться образующей, параллельной плоскости.
Проведём плоскость через окружность касания сферы Данделена и конуса до пересечения с секущей плоскостью. Прямая пересечения — директриса параболы. Покажем, что так определённые парабола, её фокус и директриса удовлетворяют геометрическому определению параболы.
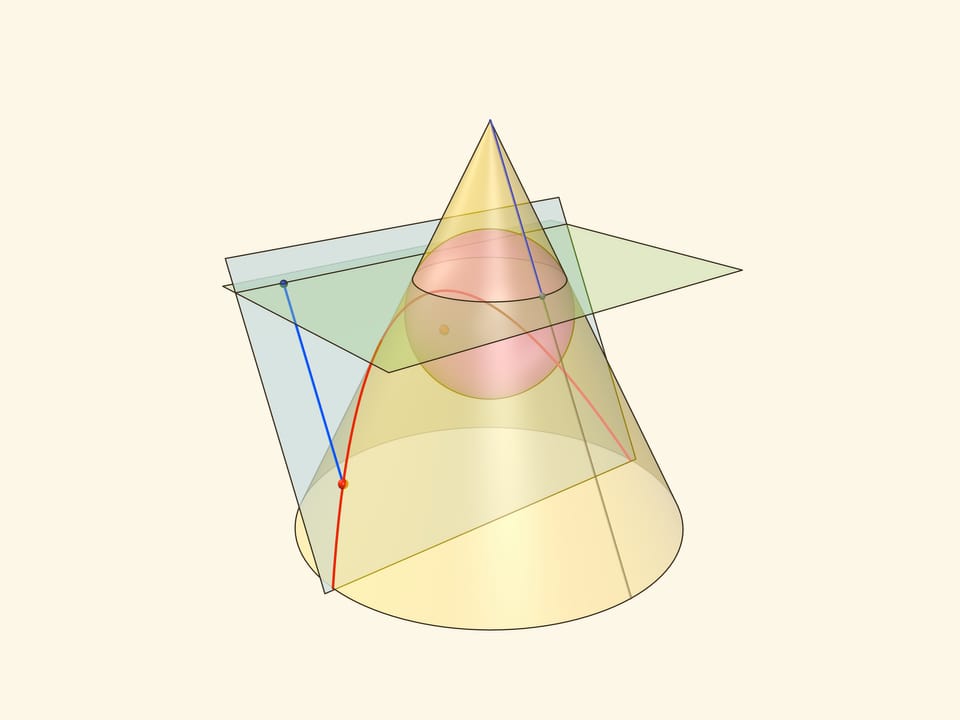
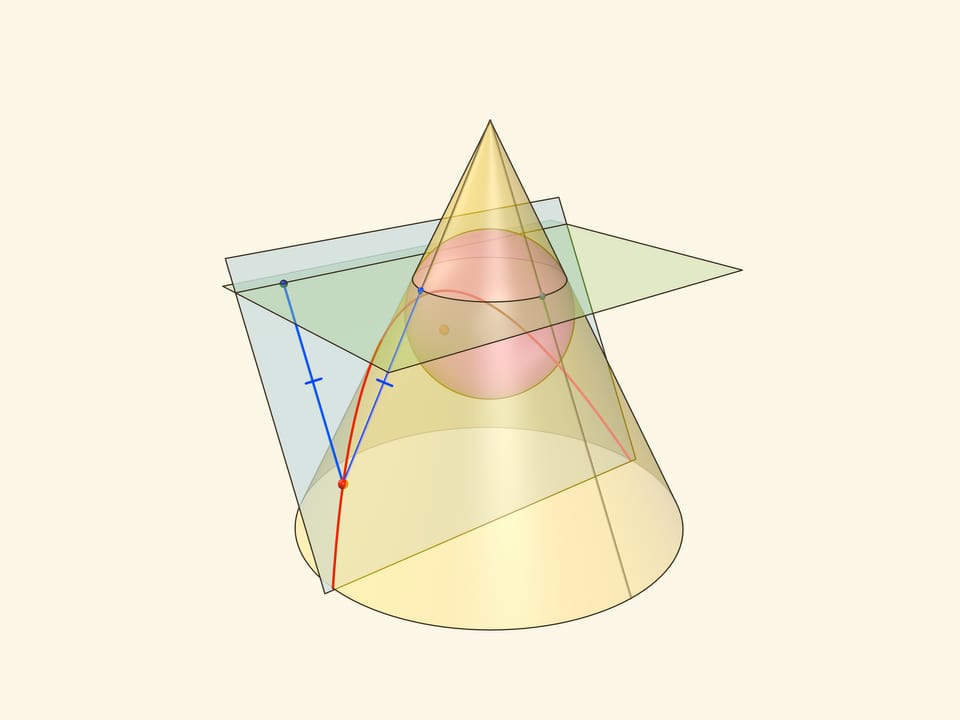
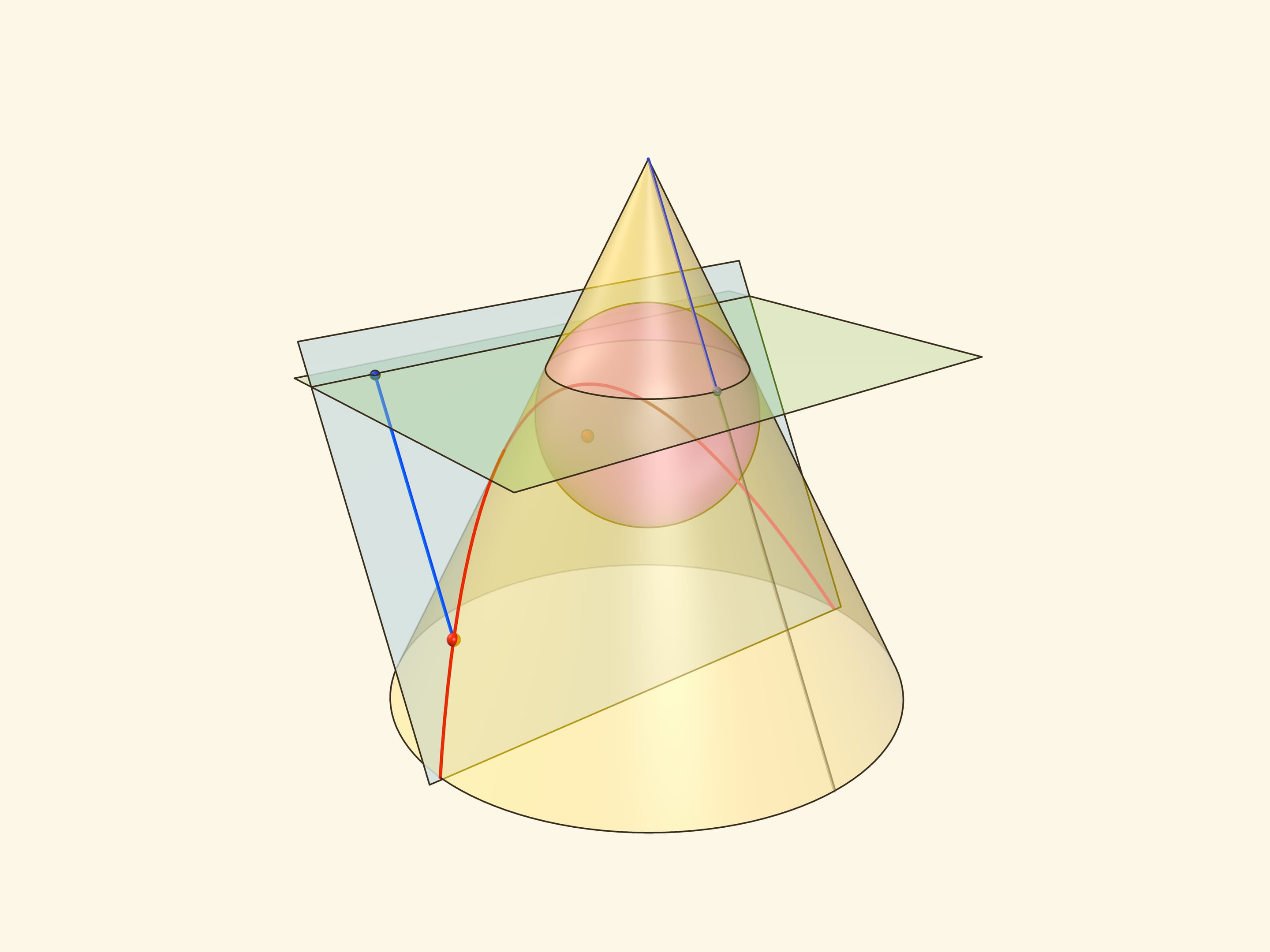
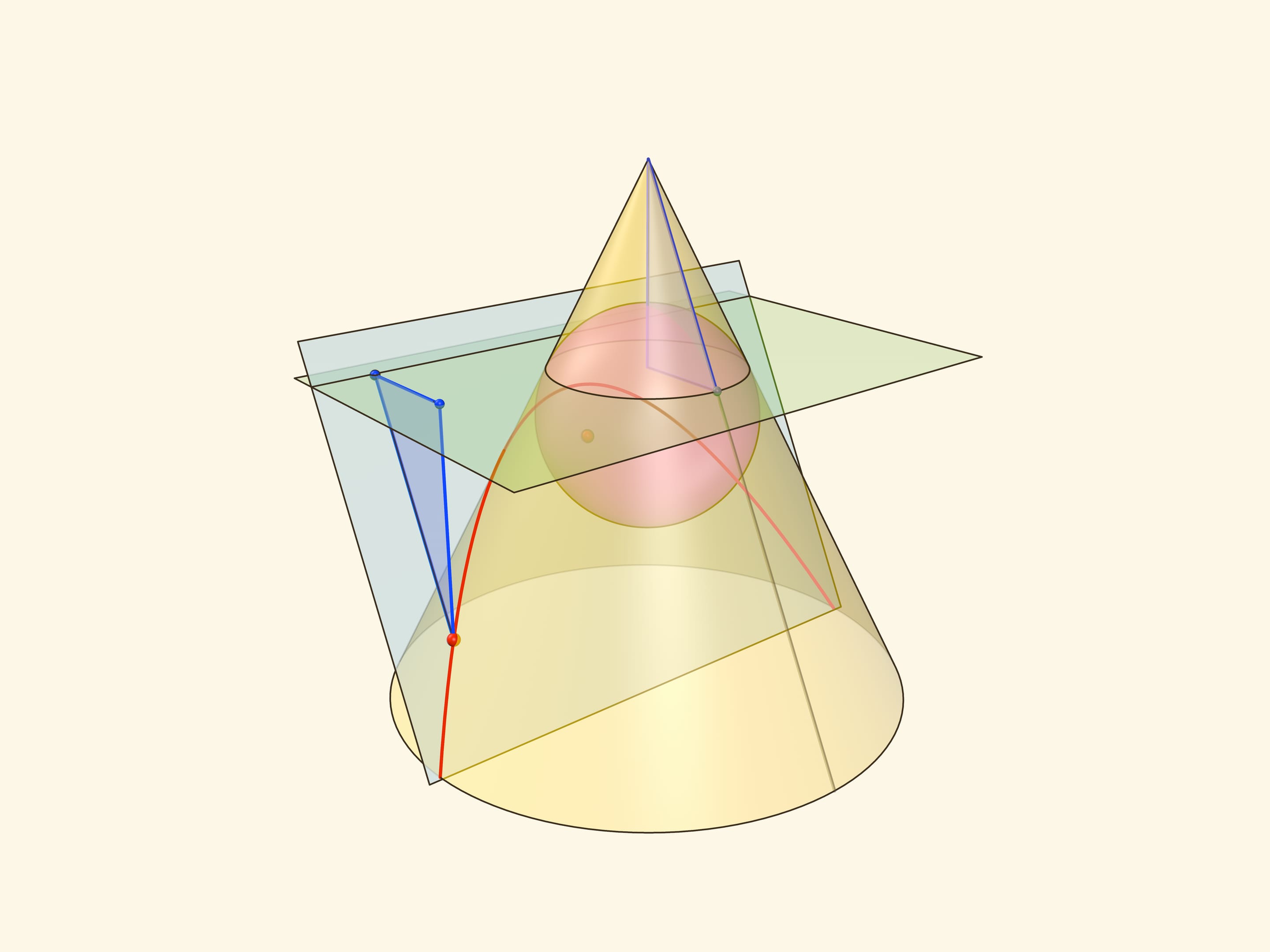
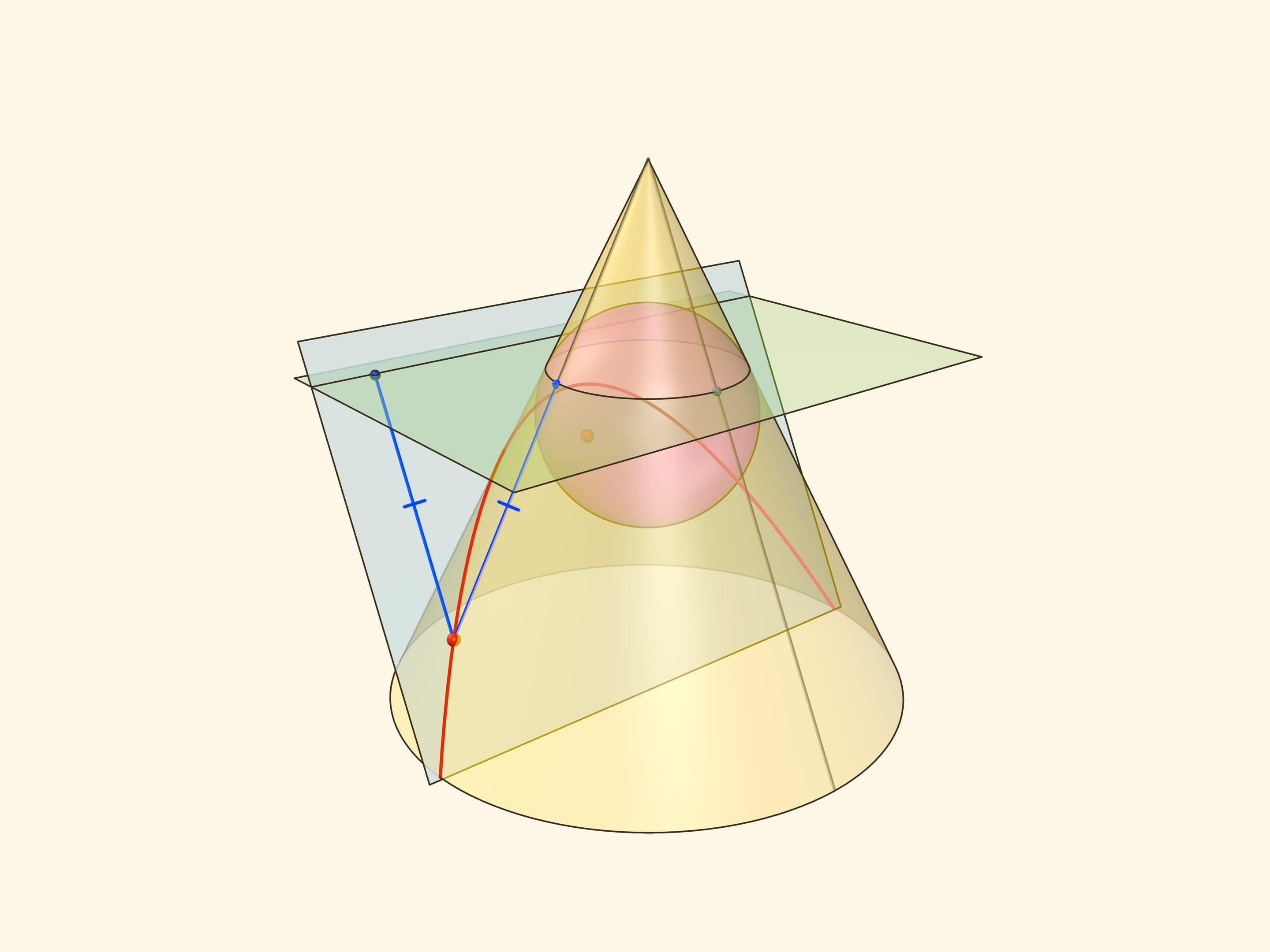
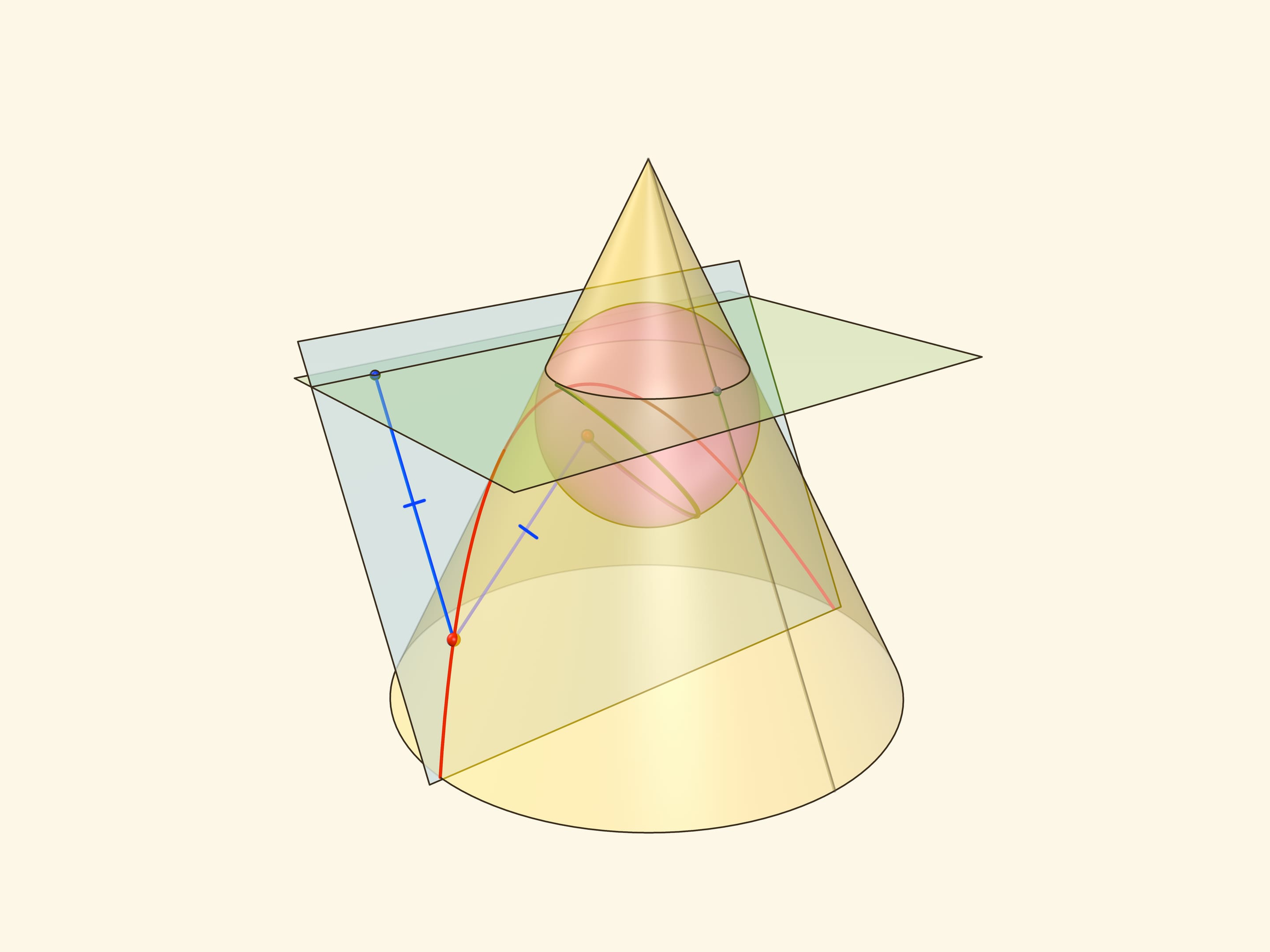
Через произвольную точку параболы проведём образующую конуса и из той же точки опустим перпендикуляры на директрису и горизонтальную плоскость. Поскольку горизонтальная плоскость перпендикулярна оси конуса, все его образующие составляют с этой плоскостью один и тот же угол, равный двугранному углу между секущей и горизонтальной плоскостями. Значит, возникшие прямоугольные треугольники равны по катету и острому углу, а поэтому равны и их гипотенузы.
Тем самым, расстояние от точки на параболе до директрисы равно расстоянию от точки до окружности касания сферы Данделена и конуса. Но последнее равно и расстоянию от точки на параболе до фокуса — как касательные к сфере, проведённые из одной точки.
Таким образом, из определения параболы как сечения конуса следует геометрическое определение параболы. У параболы геометрическое определение совпадает с определением через эксцентриситет, а значит, и оно доказано.
Гипербола как коническое сечение возникает, когда секущая плоскость пересекает обе полы конуса (иначе говоря, параллельна двум его образующим). Предлагаем читателю самостоятельно разобрать этот случай: вписать сферы Данделена в обе половинки конуса по одну сторону от плоскости и восстановить геометрические рассуждения. А мы лишь заметим, что запомнить, у эллипса или гиперболы эксцентриситет больше 1, помогает само название «гипербола»: ὑπέρ по-древнегречески означает «сверх».
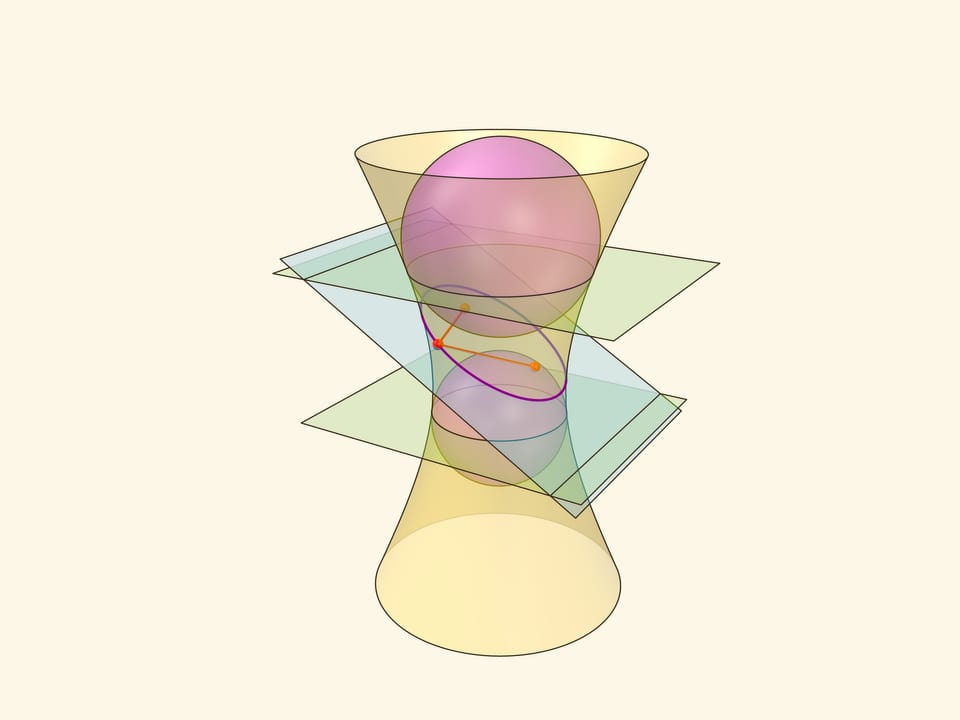
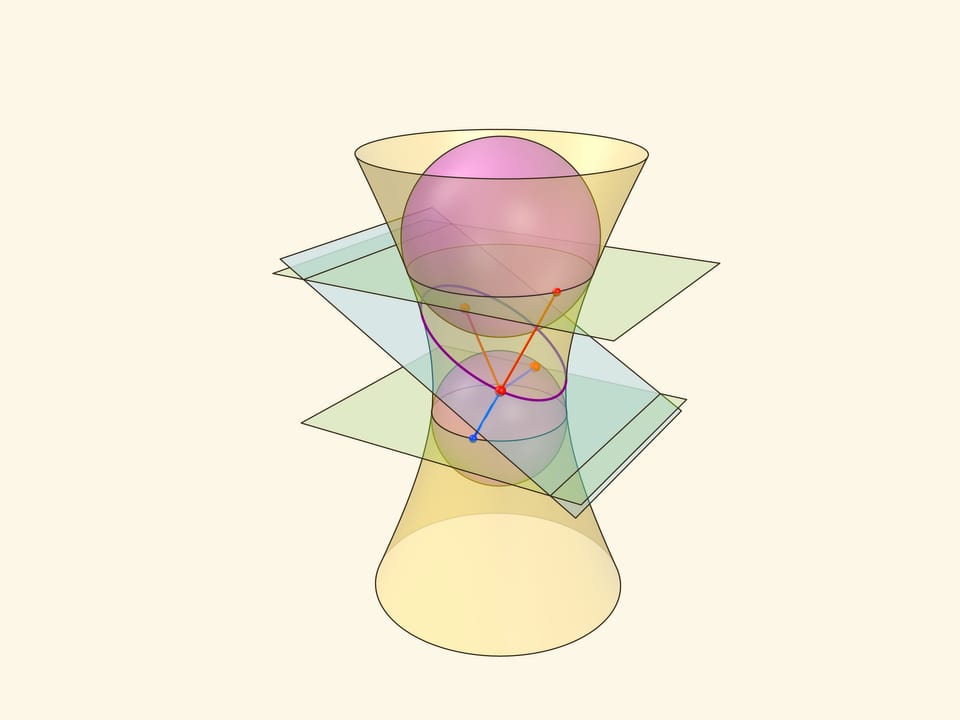
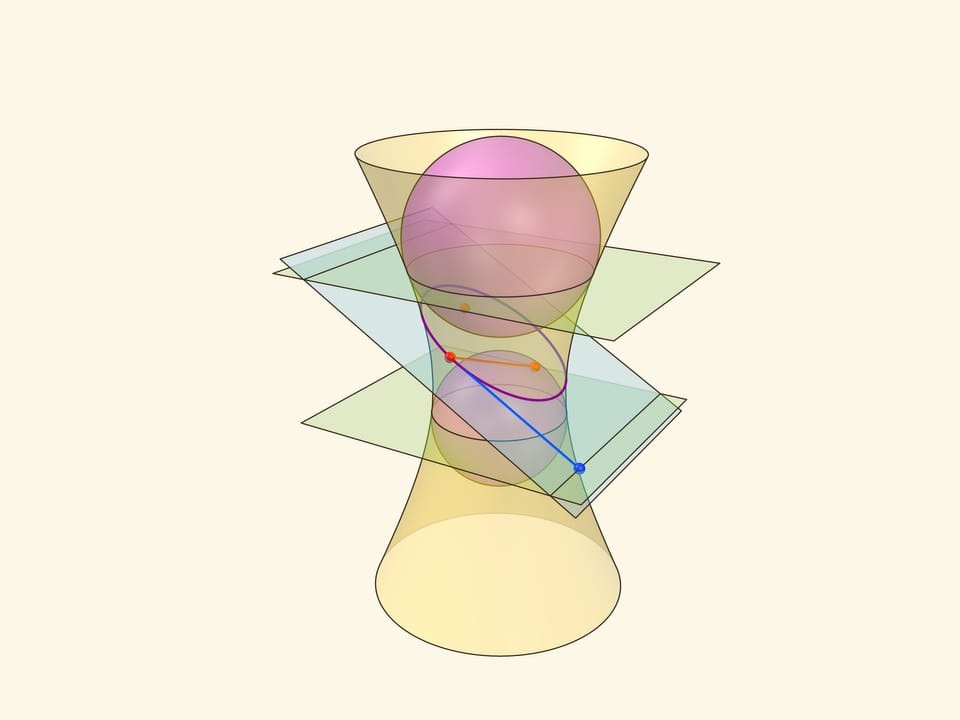
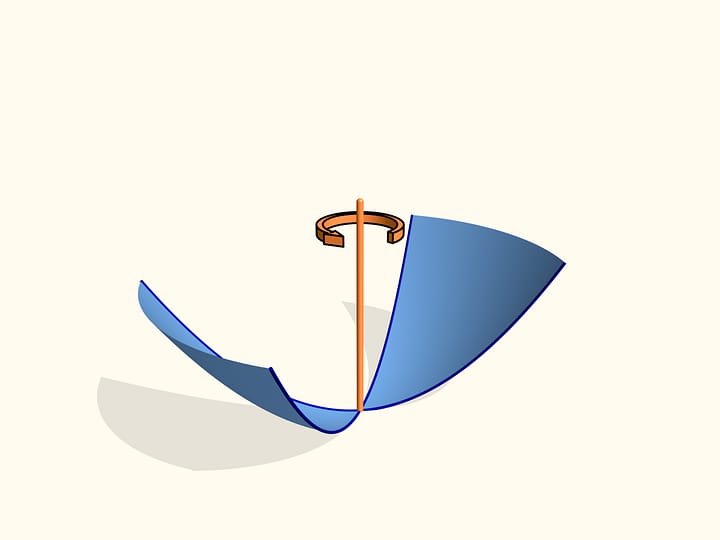
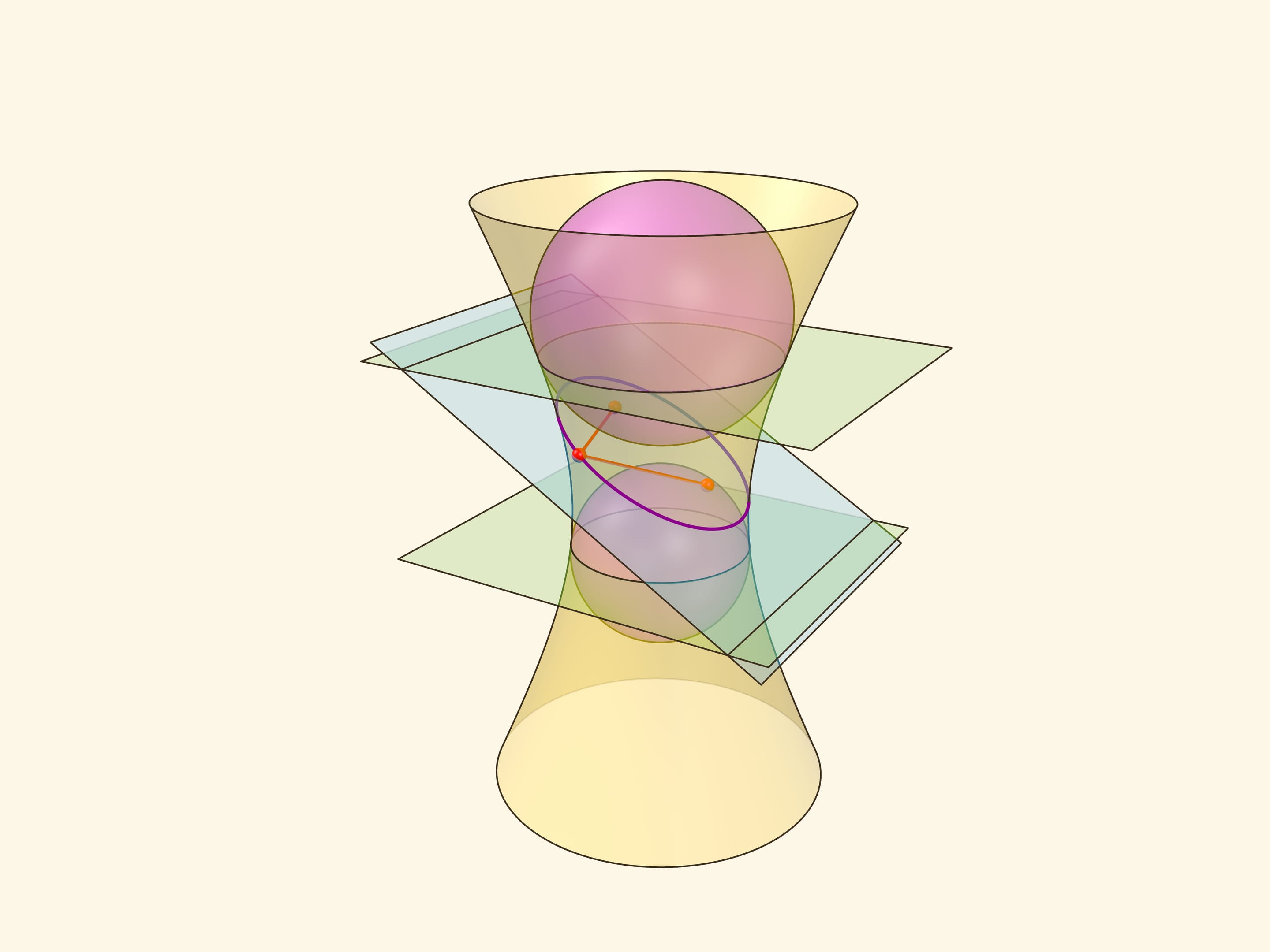
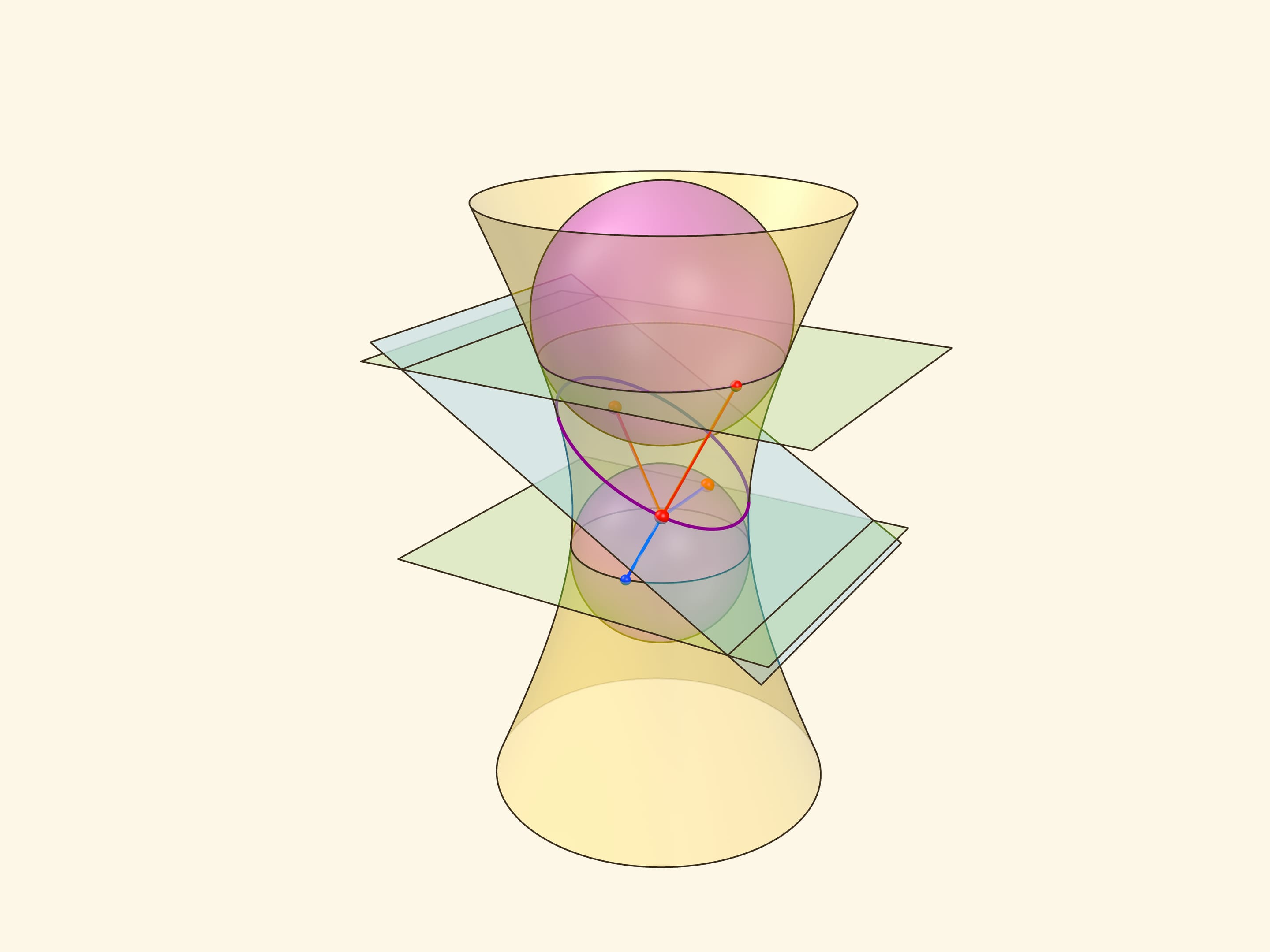
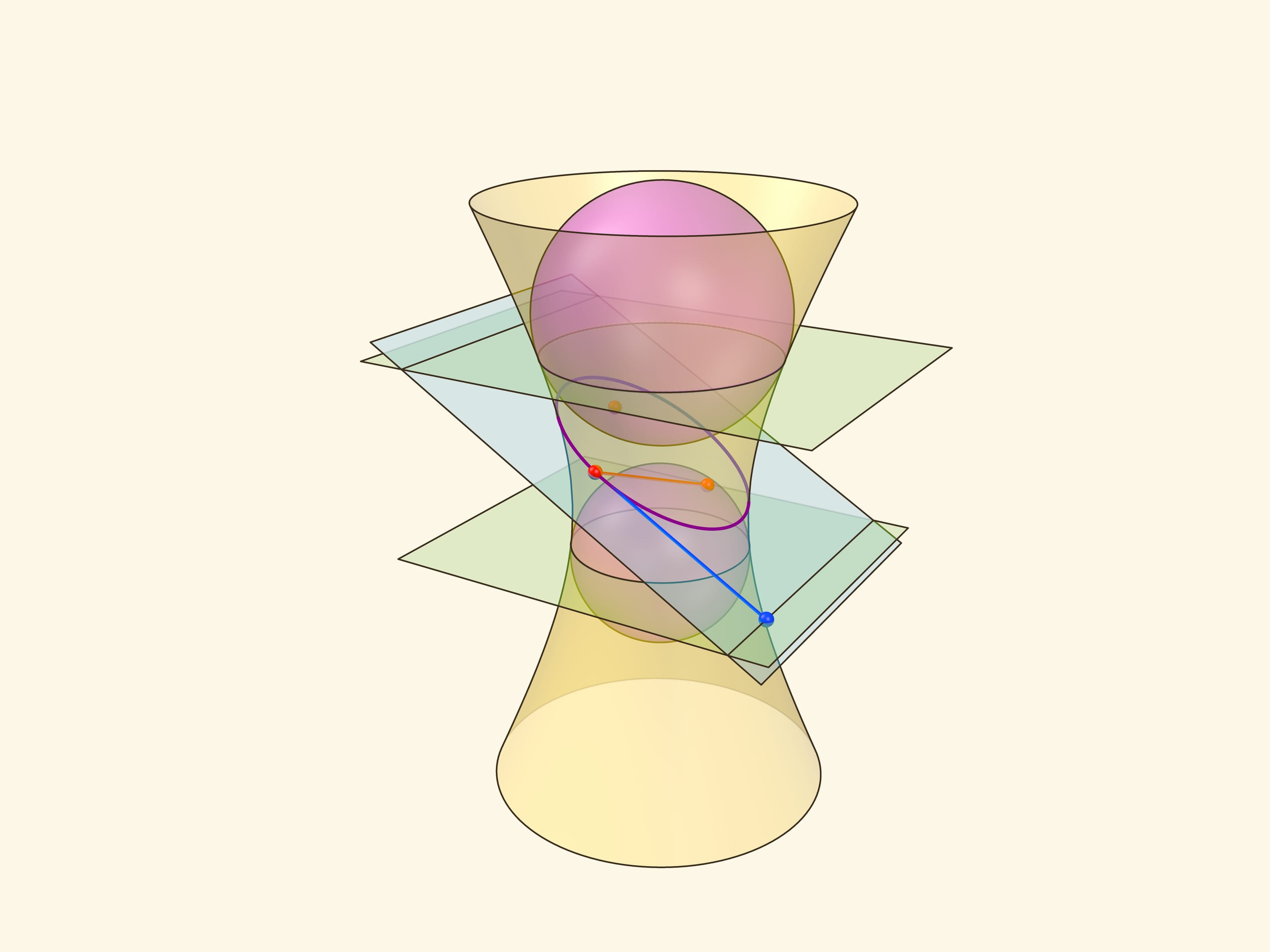
Кривые второго порядка – эллипс, параболу, гиперболу – можно получить не только как сечения конуса, но и как сечение других поверхностей второго порядка – однополостного и двуполостного гиперболоидов. А эллипс получается не только как сечение конуса или цилиндра, но и как сечение эллипсоида вращения. И конструкцию сфер Данделена можно реализовать не только в конусе и цилиндре. Первый кандидат – однополостный гиперболоид вращения: на его поверхности также есть прямолинейные образующие.
Сумма расстояний от точки на эллипсе до фокусов – точек касания сфер Данделена с секущей плоскостью — равно длине отрезка образующей, заключённого между плоскостями окружностей касания сфер Данделена с однополостным гиперболоидом. Тем самым, эта сумма всегда постоянна, и сечение является эллипсом по геометрическому определению. Можно показать, что прямые пересечения «горизонтальных» плоскостей, содержащих окружности касания сфер Данделена и гиперболоида, с плоскостью сечения являются директрисами.
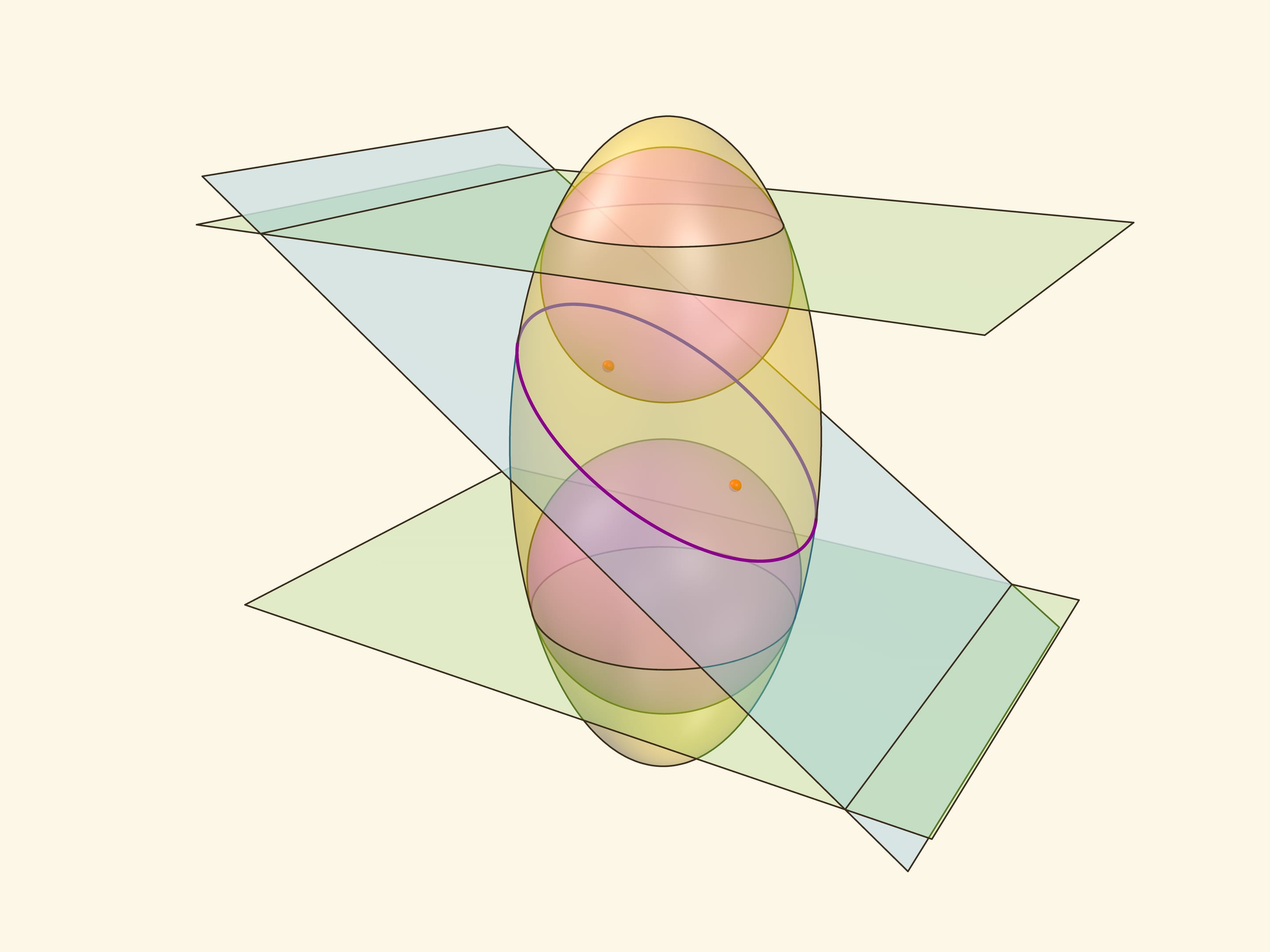
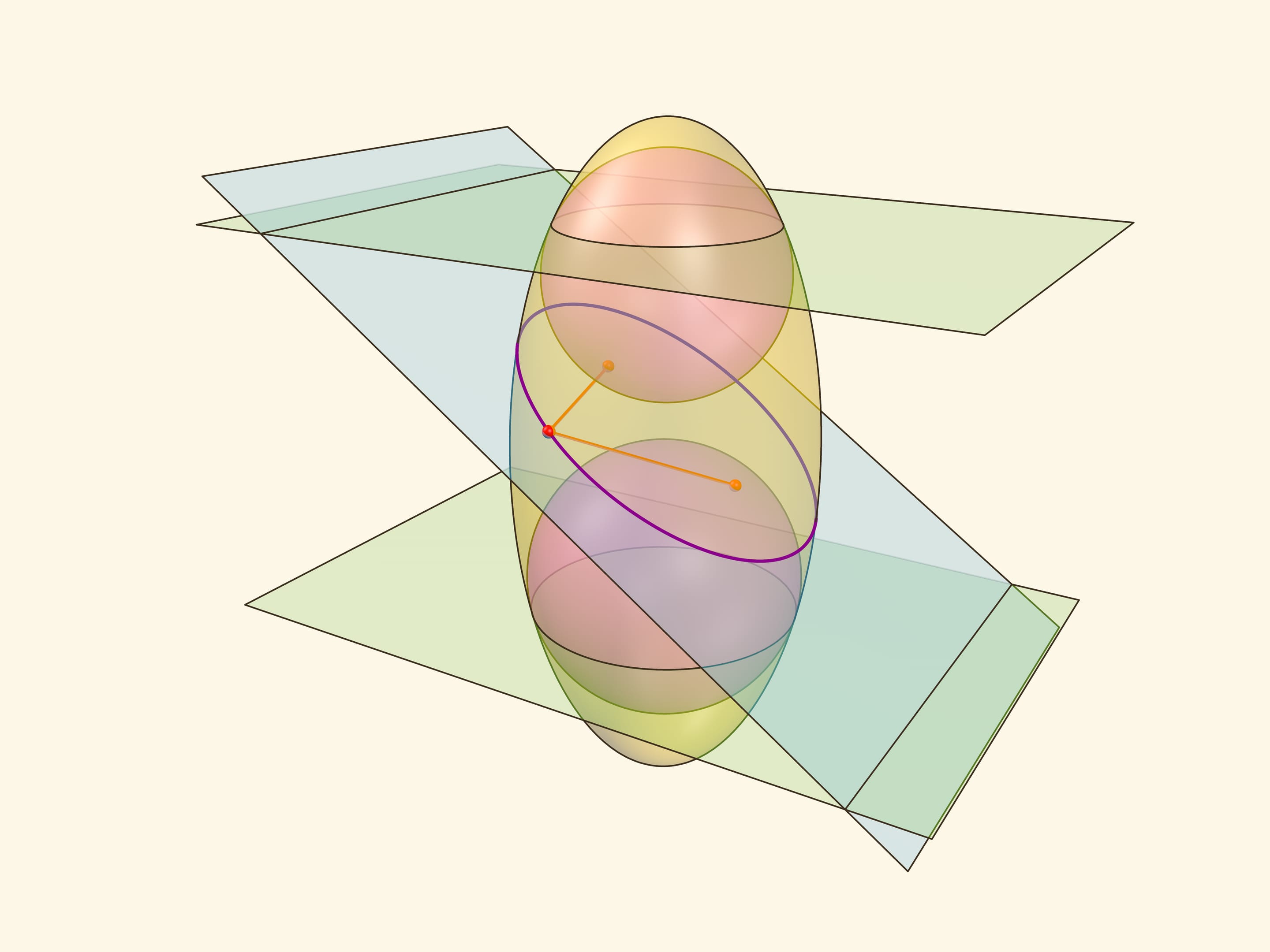
Совсем не очевидно и требует существенно более сложного доказательства тот факт, что конструкцию сфер Данделена можно обобщить на вытянутый эллипсоид вращения. Точки касания сфер Данделена с секущей плоскостью являются фокусами эллипса, лежащего в сечении эллипсоида плоскостью. А прямые пересечения «горизонтальных» плоскостей, содержащих окружности касания сфер Данделена и эллипсоида, с плоскостью сечения являются директрисами этого эллипса.
Сферы Данделена можно рассматривать и в других поверхностях вращения: параболоида и двуполостного гиперболоида.
Уже древние греки занимались изучением эллипса, гиперболы и параболы, рассматривая их как конические сечения. Аполлоний (262 до н. э. — 190 до н. э., родом из Перги, но работавший в Александрии, современник Архимеда) написал труд «Конические сечения» в восьми книгах. Термин «фокус» (лат. «очаг, огонь») был введён Иоганном Кеплером в сочинении «Оптическая часть астрономии» («Astronomiæ pars optica», 1604). А элегантную идею сфер придумал в 1822 году бельгийский математик и механик Жерминаль Данделен.
Обучаясь в лицее, Жерминаль Пьер Данделен (1794—1847) подружился с Адольфом Кетле (1796—1874); потом они будут помогать друг другу в жизни, иметь общие математические интересы и даже напишут совместную оперу.
В 1822 году Данделен опубликовал работу, в которой привёл конструкцию со сферами, вписанными в конус и касающимися плоскости конического сечения. На примере эллипса он показал равенство суммы расстояний до фокусов длине отрезка образующей. В 1826 году Данделен обобщил свою конструкцию на случай однополостного гиперболоида вращения.
Отметим, что за несколько лет до этого, в 1819 году, Адольф Кетле написал диссертацию по коническим сечениям (Dissertatio Mathematica Inauguralis, De Quibusdam Locis Geometricis, Nec Non De Curva Focali). В работе изучалась кривая, на которой лежат фокусы конических сечений, имеющих фиксированную точку конуса как вершину (т.е при изменении угла наклона плоскости сечения). И большая часть работы Данделена 1822 года посвящена именно этой кривой.
Тот факт, что прямые пересечения секущей плоскости с плоскостями, содержащими окружности касания сфер Данделена и конуса, являются директрисами эллипса, самим Данделеном отмечен не был. Это наблюдение опубликовал ирландский математик и астроном Пирс Мортон в своей статье 1829 года, где он привёл конструкцию сфер, но без ссылки на работы Данделена.
Никто из упомянутых авторов не ссылается и на трактат «De Sectionibus Conicis: Tractatus Geometricus» 1758 года ирландского математика и епископа Хью Гамильтона (1729—1805). И хотя Гамильтон не дошёл до идеи вписанных в конус сфер, касающихся плоскости сечения, он рассматривал окружности касания таких сфер и конуса. Определял он такую окружность как окружность конуса, лежащую на том же расстоянии вдоль образующей от вершины конического сечения, на котором от неё находится фокус. Для такой окружности он доказал оба факта: для любой точки конического сечения длина образующей до окружности равна расстоянию до фокуса; плоскость, содержащая такую окружность, пересекается с плоскостью сечения по директрисе. Причём доказал для всех трёх типов конических сечений — эллипса, параболы и гиперболы. По словам писателя Джеймса Уиллса, в этой книге Гамильтон «был первым, кто вывел свойства конического сечения из свойств конуса с помощью общих демонстраций, не обременённых леммами и протекающих в более естественном и наглядном порядке». Трактат получил признание за ясность изложения, а Леонард Эйлер назвал его идеальной книгой.
Литература
Розенфельд Б. А. Аполлоний Пергский. — М.: МЦНМО 2004.
Гильберт Д.,
Нилов Ф. Обобщение теоремы Данделена (к 200-летию доказательства) // Журнал «Квант». — [в печати].
Плакат «Конические сечения» // ИПС «Задачи по геометрии».
Dandelin M. G. Mémoire sur quelques propriétés remarquables de la focale parabolique // Nouveaux mémoires de l'Académie royale des sciences et belles-lettres de Bruxelles. — 1822. — Tome II. — P. 171—202 + illustrations.
Dandelin M. G. Mémoire sur l’hyperbolöıde de révolution, et sur les hexagones de Pascal et de M. Brianchon // Nouveaux mémoires de l'Académie royale des sciences et belles-lettres de Bruxelles. — 1826. — Tome III. — P. 1—14 + illustrations.