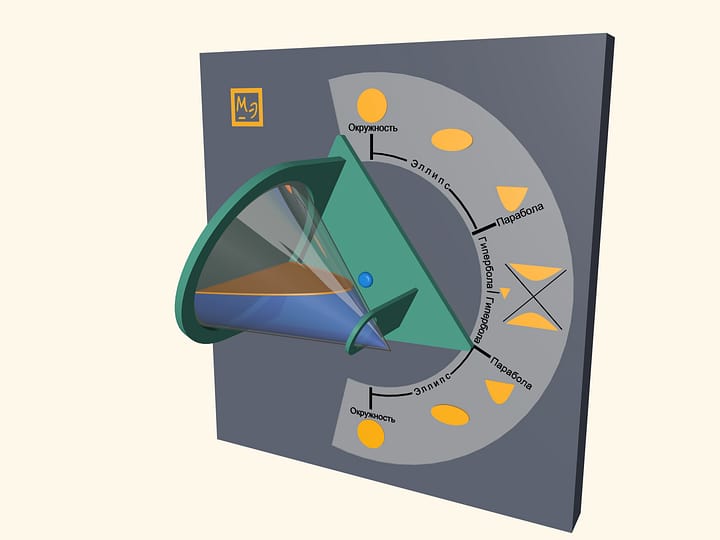
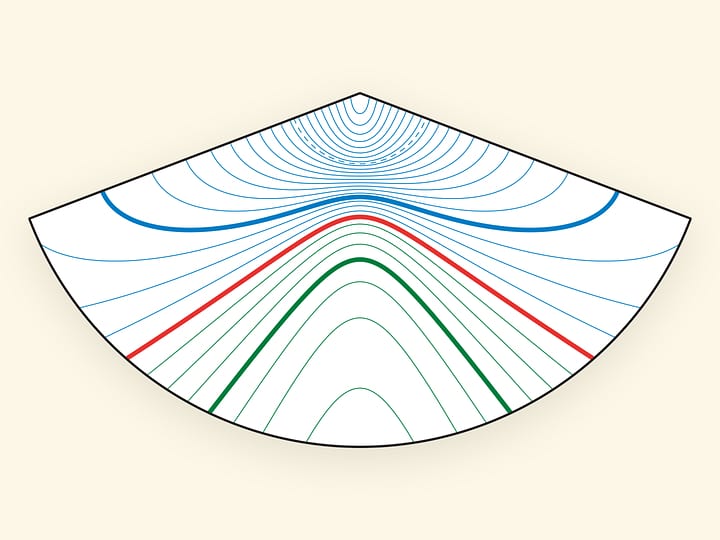
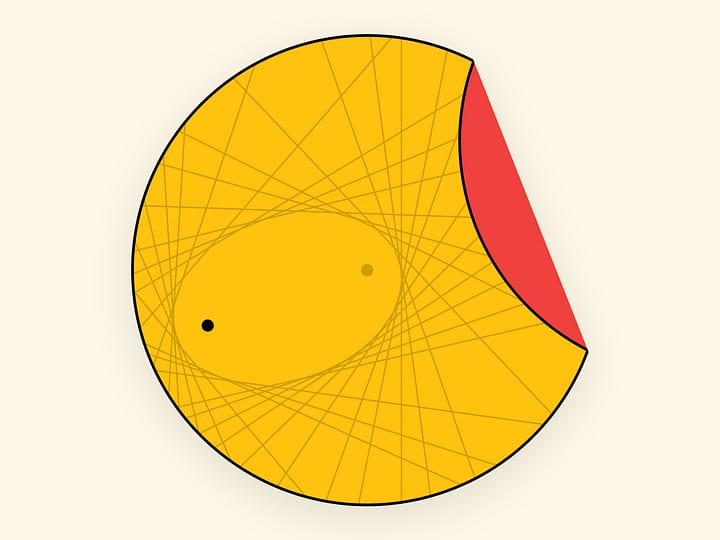
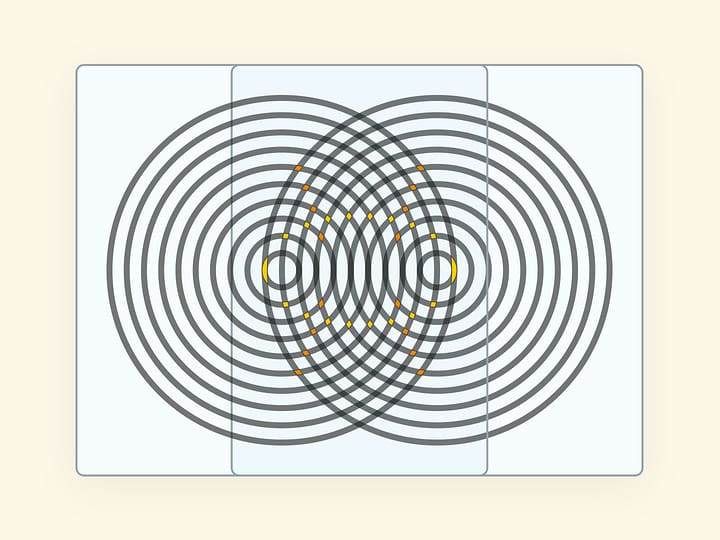
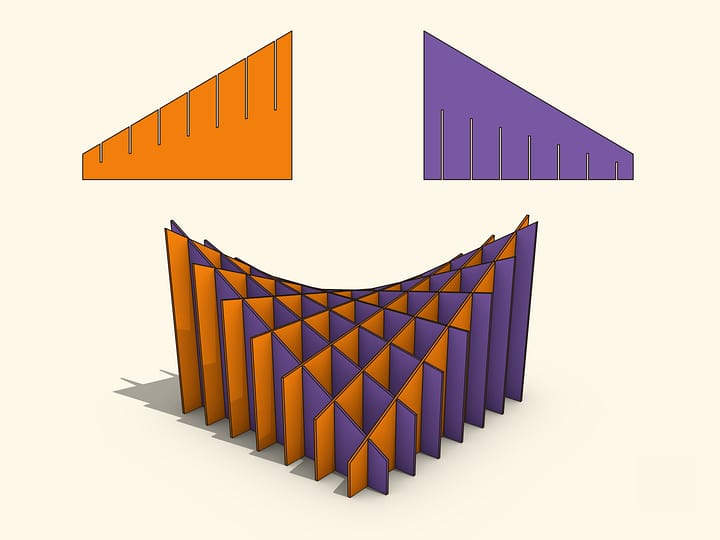
Упакованные в цилиндрические тубусы чипсы, чтобы они меньше крошились, запекают на жарочных листах, придающих плоским заготовкам форму гиперболического параболоида — поверхности второго порядка.
Гиперболический параболоид изогнут, похож на седло, но при этом является линейчатой поверхностью! По определению, линейчатая поверхность может быть образована непрерывным движением прямой линии, называемой образующей.
Через каждую точку гиперболического параболоида, так же как и однополостного гиперболоида, проходят две прямые.
Свойство линейчатости можно наглядно продемонстрировать, используя чипсы, упакованные в тубусы.
Проделайте в крышке тубуса прямолинейную прорезь. Возьмите из стопки чипсов один ломтик и опустите его в тубус через полученную щель. Это можно сделать, не сломав ломтик, надо только опускать и поворачивать его так, чтобы в каждый момент времени через прорезь проходила образующая гиперболического параболоида.
«На заметку»: порядок слов в названии «гиперболический параболоид» можно запомнить по первым буквам слов — они идут в алфавитном порядке, как в русском, так и в английском алфавитах.
Литература
Чипсы // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 90.